¿Sabías que puedes navegar las publicaciones deslizando a la izquierda y la derecha?

Estática

09 May 2018 . category: .

Estática

Es la rama de la física que se estudia a los cuerpos en equilibrio. Esta rama es parte de la dinámica solo que estudia el caso en el cual el valor de la aceleración es igual a cero.

Equilibrio

Un cuerpo está en equilibrio si no tiene aceleración, esto es, si la aceleración de un cuerpo es cero. O un cuerpo está en equilibrio cuando la suma de las fuerzas externas que actúan sobre es cero.

El equilibrio se puede clasificar en equilibrio estático cuando el cuerpo permanece en reposo y en equilibrio dinámico cuando el cuerpo tiene un movimiento rectilíneo uniforme.

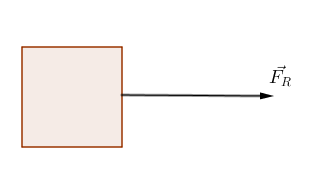
La fuerza resultante fue definida como una fuerza única cuyo efecto es el mismo que el de un sistema dado de fuerzas.

Equilibrio de una partícula

Para simplificar el estudio de este tipo de cuerpos es equilibrio se pueden despreciar sus dimensiones y considerarse como una partícula.

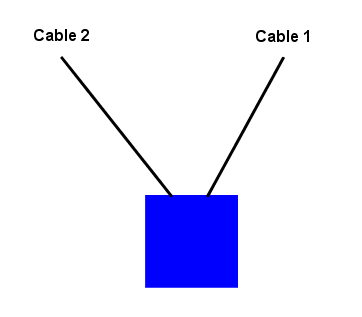
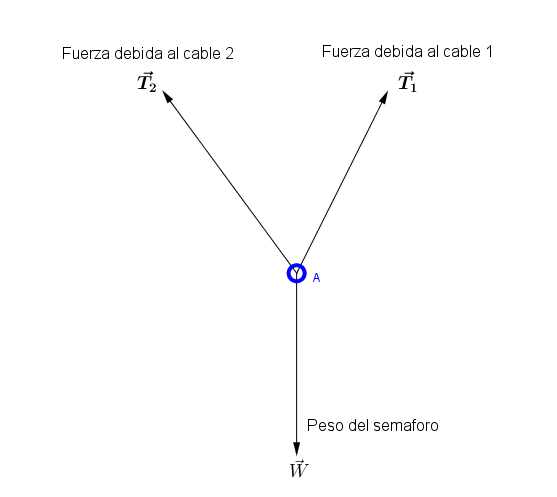
Condición de Equilibrio

Una partícula está en equilibrio cuando la suma vectorial de todas las fuerzas que actúan sobre ellas es igual a cero. Ya que de acuerdo con la segunda ley de Newton si la fuerza neta es igual a cero, entonces la aceleración es igual a cero. Matemáticamente:

$\overrightarrow{F_{n}} = 0$

En función de todas las fuerzas actuantes:

$\overrightarrow{F_{1}} + \overrightarrow{F_{2}} + \overrightarrow{F_{3}} + \ldots + \overrightarrow{F_{N}} = 0$

O lo que es lo mismo:

$\sum_{i = 1}^{N}{\overrightarrow{F_{i}} = 0}$

En donde:

$\sum = \ suma\ de\ldots$ $\overrightarrow{F_{i}} = fuerza\ i\ sobre\ la\ particula$ $\overrightarrow{F_{N}} = fuerza\ enecima\ sobre\ la\ particula$

Expresando la ecuación anterior en función de componentes rectangulares de las fuerzas:

$\sum F_{x}=0$ $\sum F_{y}=0$

Ejemplo:

Una persona que pesa 800N descansa sobre una hamaca. La cuerda cercana a la cabeza de la persona hace un ángulo α de 25° con la horizontal, mientras que la cuerda que se encuentra en los pies hace un ángulo $\theta$ de 40° con la horizontal. Determina la magnitud de las tensiones que ejercen las cuerdas.

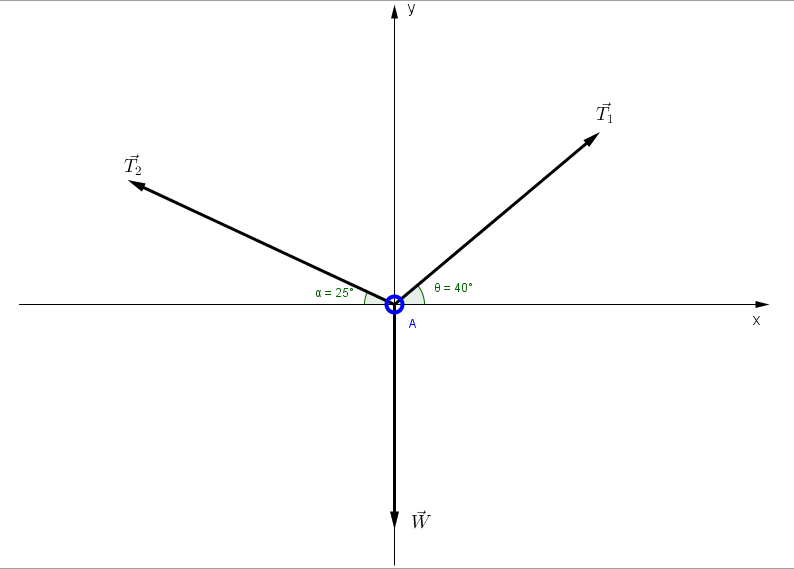
Solución:

Para determinar las componentes rectangulares de las fuerzas, determinamos los ángulos que hacen dichas fuerzas con el eje x, es decir para T2 el ángulo será 180-25=155°, y para W será de 270°.

Emplearemos la siguiente tabla:

Al aplicar las ecuaciones de condición de equilibrio:

$\sum F_{x} = 0.766T_{1} - 0.906T_{2} = 0$ $\sum Fy = 0.642T_{1} + 0.423T_{2} - 800 = 0$

Despejamos T1:

$T_{1} = \frac{0.906\ T_{2}}{0.766\ }$

Sustituyendo:

$0.642\left( \frac{0.906}{0.766} \right)T_{2} + 0.423\ T_{2} - 800 = 0$ $1.182\ T_{2} = 800$

Despejamos T2:

$T_{2} = 676.81\ N$

Sustituimos:

$T_{1} = \ \frac{0.906}{0.766}\left( 676.81 \right)$ $T_{1} = 800.51N$

Fuerza resultante y fuerza equilibrante

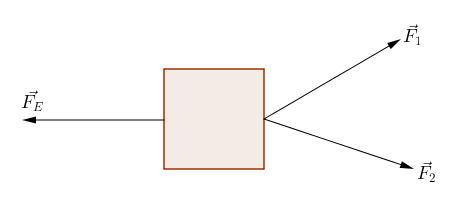
Cuando un cuerpo o una partícula está sometido a la acción de varias fuerzas y se quiere conocer las fuerza que hay que aplicar para que dicho cuerpo permanezca en equilibrio, lo que se determina primero es la fuerza resultante, es decir la fuerza que puede sustituir a dichas fuerzas cuando actúan simultáneamente, ya que produce el mismo efecto que ellas. Conocidas esta fuerza, la fuerza equlibrante será la fuerza de igual magnitud y dirección que la resultante pero, de sentido contrario.

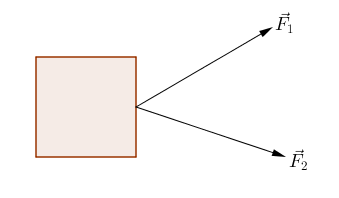
Momento de una fuerza o torque

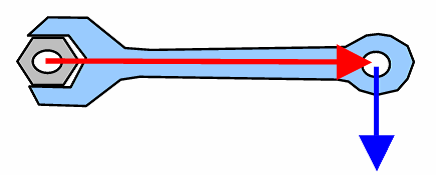
Es una magnitud física que indica la capacidad de una fuerza para producir rotación a un cuerpo y se representa por la letra griega τ (tau).

El momento de fuerza depende tanto de la magnitud de la fuerza aplicada y de la distancia del eje de giro del cuerpo al punto de aplicación de la fuerza como del ángulo entre la fuerza y la línea que une al eje de giro con el punto de aplicación.

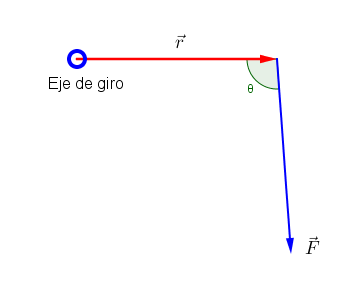
Resultado de imagen para llave tuerca torque

El momento de fuerza es una magnitud vectorial cuya magnitud se puede obtener por:

$\tau = rF\sin\theta$

En el SI, la unidad del momento de fuerza o torque es el newton-metro (Nm).

Ejemplo:

Un técnico ejerce una fuerza de 80N en el extremo de una llave inglesa de 20cm. Si esta fuerza forma una ángulo de 70° con el mango de la llave, ¿Cuál es la magnitud del momento de fuerza producido en la tuerca?

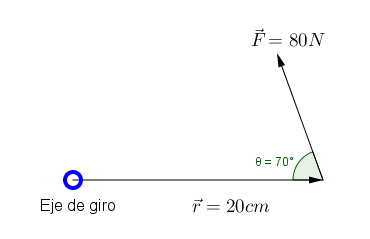
Solucion:

La magnitud se calcula por:

$\tau = rF\sin\theta$

Al sustituir valores:

$\tau = \left( 0.20m \right)\left( 80N \right)\sin{70}$ $\tau = 15Nm$

Momento de fuerza resultante

El momento resultante se obtiene de sumar algebraicamente los momentos de fuerza positivos y negativos debidos a cada fuerza. Matemáticamente:

$\tau_{R} = \sum \tau$

Ejemplo:

Determina el momento de fuerza resultante sobre un sube y baja, si uno de los niños pesa 250N y se encuentra a 0.70m del eje de giro. El otro niño pesa 220N y se encuentra a 1.5 m del eje de giro.

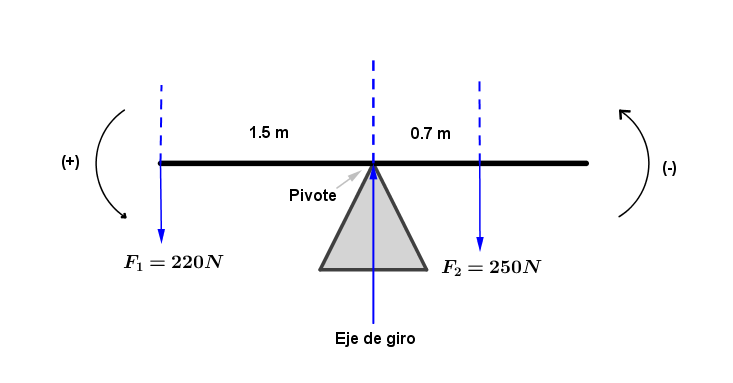
Solución:

Primero elaboramos un diagrama de cuerpo libre

Datos:

$r_{1} = 1.5\ m$ $r_{2} = 0.7m$ $F_{1} = 220N$ $F_{2} = 250N$ $\overrightarrow{\tau_{r}} = \overrightarrow{\tau_{1}} + \overrightarrow{\tau_{2}}$ $\tau = r_{1}F_{1} - r_{2}F_{2}$ $\tau = \left( 1.5m \right)\left( 220N \right) - \left( 0.7m \right)\left( 250N \right)$ $\tau = 155\ Nm$

Par de fuerzas

Cuando dos fuerzas de igual magnitud y sentidos contrarios actúan sobre el mismo punto de un cuerpo rígido, este permanecerá en equilibrio, pero si estas fuerzas se aplican en untos diferentes, de manera que sus líneas de acción sean paralelas, el cuerpo girara.

Dos fuerzas de igual magnitud pero opuestas y cuyas líneas de acción sea paralelas constituyen un par de fuerzas. El momento resultante es independiente de la elección del punto a partir del cual se miden las distancias. La magnitud del momento de fuerza resultante se obtiene de la siguiente ecuación:

$\tau = Fd$

Donde

$F = magnitud\ de\ las\ fuerzas\ actuantes\ en\ el\ par$ $d = distancia\ entre\ las\ dos\ fuerzas$

Ejemplo:

Sobre un volante de 60cm de diámetro se aplica un par de fuerzas. La magnitud de las fuerzas aplicadas es de 30N. ¿Cuál es la magnitud del momento de fuerza resultante?

Solución:

$d = 60cm = 0.6m$ $F = 30N$

Formula:

$\tau = Fd$ $\tau = \left( 30N \right)\left( 0.6m \right)$ $\tau = 18Nm$

Equilibrio de cuero rígido

Un cuerpo rígido es aquel en el que las distancias entre dos de sus puntos cualquiera permanecen constantes, es decir, no se deforman por la acción de fuerzas externas.

Un cuerpo rígido debe satisfacer las siguientes condiciones para estar en equilibrio.

1.- Equilibrio de traslación. La suma vectorial de todas las fuerzas que actúan sobre el cuerpo debe ser cero.

$$\sum \overrightarrow{F} = 0

En función de sus componentes:

$\sum \overrightarrow{F_{x}} = 0$ $\sum \overrightarrow{F_{y}} = 0$

2.- Equilibrio de rotación. Para que un cuerpo rígido se encuentre en equilibrio, la fuerza resultante debe ser cero y el momento de fuerza resultante también debe de ser cero.

$\sum \overrightarrow{\tau} = 0$

Docente de Física 1 y TICs, Ing. en Computación egresado de la UNAM