¿Sabías que puedes navegar las publicaciones deslizando a la izquierda y la derecha?

Movimiento Rectilíneo

02 Apr 2018 . category: .

Movimiento Rectilíneo Uniforme

El movimiento rectilíneo uniforme (MRU) es aquel que describe un cuerpo que se mueve en línea recta y con una velocidad constante, es decir, recorre distancias iguales en intervalos de tiempos iguales.

Es el movimiento donde se recorren distancias iguales en tiempos iguales, siendo la trayectoria una línea recta.

Ley de posiciones:

$d = d_{0} + vt$

Donde:

$d = distancia\ final$ $d_{0} = distancia\ inicial$ $v = velocidad$ $t = tiempo$

Debido a que el cuerpo se mueve en línea recta, la distancia recorrida y el desplazamiento son iguales en magnitud por lo que la velocidad, la velocidad media, la rapidez y la rapidez media adoptarán el mismo valor. Por esta razón, será indistinto, para este tema, el uso de estos términos por lo que utilizaremos una misma fórmula para su cálculo, exceptos por lo ejemplos donde se especifique.

$\overrightarrow{v} = \frac{\overrightarrow{d}}{t}$

Gráficas del MRU

Gráfica Posición-Tiempo

El movimiento rectilíneo uniforme puede ser representado gráficamente utilizando un plano cartesiano, en donde el eje de las abscisas es sustituido por el tiempo, mientras que el eje de las ordenadas por la distancia. Es necesario aclarar que si recurrimos a una gráfica es porque nos permite analizar fácil y rápidamente los datos que muestra.

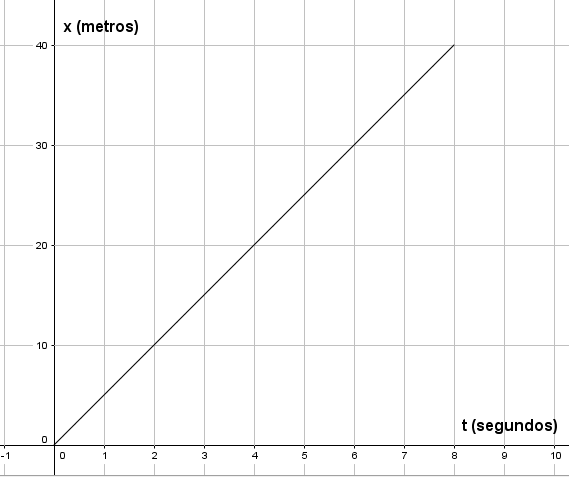
El móvil parte del origen y se aleja de el a una velocidad constante de 5 [m/s]. La gráfica es una recta ascendente. Como $x_{i} = 0$ , la posición del móvil, en cada instante, será $x = 5t$ .

El espacio recorrido y el tiempo transcurrido por el móvil son proporcionales por lo que la gráfica será siempre una línea recta cuya inclinación o pendiente nos indica el valor de la rapidez con que se mueve el cuerpo. Entre mayor pendiente presente la gráfica mayor será la rapidez del cuerpo y viceversa a menor pendiente menor rapidez.

Gráfica Velocidad-Tiempo

Si queremos realizar una gráfica velocidad contra tiempo debemos colocar en el eje de las abscisas del plano cartesiano al tiempo y a la velocidad en lugar de las ordenadas. El área que queda debajo de la recta será la distancia que recorra el móvil puesto que d=vt.

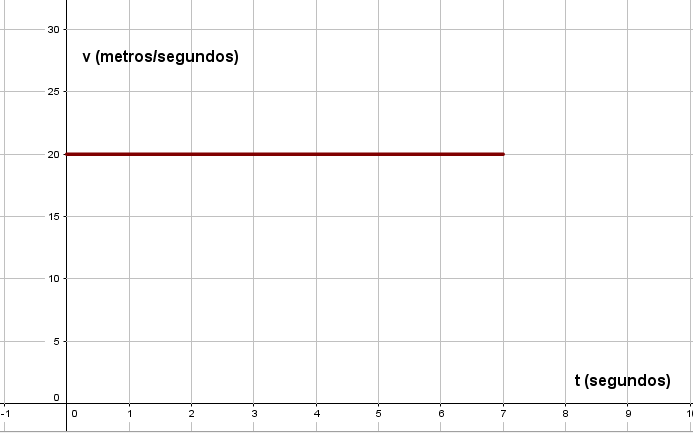
Esta gráfica muestra el movimiento de un objeto que se mueve a una velocidad constante de 20[km/h].

La gráfica velocidad-tiempo es una línea horizontal puesto que la velocidad en el M.R.U. no cambia.

Ejemplo:

Un móvil viaja describiendo un M.R.U. y por cada 2 segundos avanza 5 metros.
Realizar una gráfica d-t en donde el móvil parta del origen y otra v-t calculando el área
debajo de la gráfica para obtener la distancia recorrida para un intervalo de 0-10 segundos.

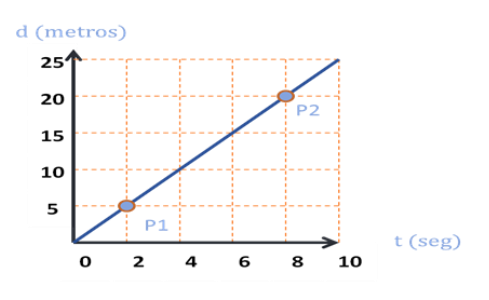
Como la pendiente de la recta es igual a la velocidad, entonces, utilizaremos la fórmula de ésta para dos puntos cualquiera, por ejemplo P1(2,5) y P2(8,20) y el resultado será nuestra velocidad:

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ $v = \frac{d_{2} - d_{1}}{t_{2} - t_{1}}$

Sustituyendo:

$v = \frac{20m - 5m}{8s - 2s} = \frac{15m}{6s} = 2.5m/s$

Construyamos ahora la gráfica velocidad contra tiempo con el valor obtenido.

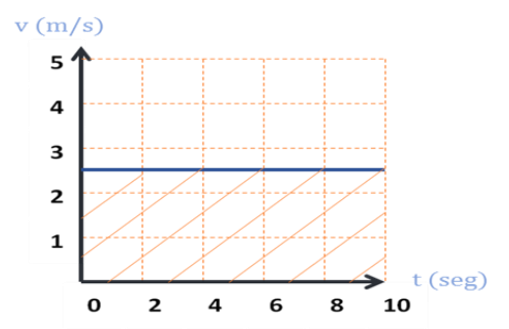
El área debajo de la recta se calcula multiplicando la base que son los 10 segundos por la altura que corresponde al valor de la velocidad de 2.5 m/s. Dando un resultado de 25 m. comprobando el valor que en un inicio calculamos en la tabla posición-tiempo.

Aceleración

Consideremos movimiento en una sola dimensión. Los cambios en la velocidad pueden ser positivos o negativos; su dirección la indicaremos con los signos más y menos.

Así como la velocidad describe la tasa de cambio de posición con el tiempo, la aceleración describe la tasa de cambio de velocidad con el tiempo. Al igual que la velocidad, la aceleración es una cantidad vectorial. En el movimiento rectilíneo, su única componente distinta de cero está sobre el eje en que ocurre el movimiento.

Aceleración: es el cambio de velocidad de un objeto o móvil en un intervalo de tiempo dado. Es una cantidad vectorial, porque consta de una magnitud o valor, dirección y sentido.

Su fórmula es;

$aceleracion = \frac{\text{cambio de velocidad}}{\text{intervalo de tiempo}}$ $a = \frac{v_{f} - v_{i}}{t}$

Su unidad es m/s^2.

La velocidad inicial ( $v_{i}$ ) del cuerpo se define como la velocidad del móvil al inicio del intervalo de tiempo, y que si el móvil se encuentra en reposo, esta velocidad tiene un valor de cero. La velocidad final ( $v_{f}$ ) se define como la velocidad al terminar el intervalo de tiempo.

Se considera que un móvil tiene una aceleración positiva cuando aumenta su velocidad. Si disminuye su velocidad tiene aceleración negativa (desaceleración o frenado). De igual modo se considera que un cuerpo no tiene aceleración (a=0) si está inmóvil o si se mueve con velocidad constante (a = 0).

Cuando se resuelven problemas donde esté involucrada una aceleración constante, es importante elegir la fórmula correcta y sustituir los datos conocidos. Los problemas se refieren frecuentemente al movimiento de un móvil que parte del reposo o que se detiene después de cierta velocidad.

Las siguientes son las fórmulas más utilizadas en el movimiento rectilíneo uniformemente acelerado:

$a = \frac{v_{f} - v_{i}}{t}$ $a = \frac{v_{f}^{2} - v_{i}^{2}}{2d}$ $d = \left( \frac{v_{i} + v_{f}}{2} \right)t$ $d = v_{i}t + \frac{1}{2}at^{2}$

Y de aquí se puede despejar cualquier variable según se necesite.

Ejemplo:

Un automóvil en una carretera recta acelera de 2.18m/s a 16.66m/s en 8.0s ¿Cuál es el valor de aceleración en dicho intervalo?

Solución:

$v_{0} = 2.18m/s$ $v = 16.66m/s$ $t - t_{0} = t = 8.0s$

Formula:

$a = \frac v-v _{0}{t}$ $a = \frac{16.66\frac{m}{s} - 2.18\frac{m}{s}}{8s} = 1.81\frac{m}{s^{2}}$

Aceleración media

Consideremos otra vez el movimiento de una partícula en el eje x. Suponga que, en el tiempo t_1, la partícula está en el punto P_1 y tiene una componente x de velocidad (instantánea) v_1x, y en un instante posterior t_2 está en P_2 y tiene una componente x de velocidad v_2x. Así, la componente x de la velocidad cambia en v_x = v_2x - v_1x en el intervalo t = t_2 - t_1.

Definimos la aceleración media de la partícula al moverse de P_1 a P_2 como una cantidad vectorial cuya componente x es a_med x igual a v_x, el cambio en la componente x de la velocidad, dividido entre el intervalo de tiempo t:

$a_{med - x} = \frac{v_{2x} - v_{1x}}{t_{2} - t_{1}} = \frac{v_{x}}{t}$

Aceleración instantánea

Ya podemos definir la aceleración instantánea con el mismo procedimiento que seguimos para la velocidad instantánea. Para definir la aceleración instantánea en P1, tomamos el segundo punto P2, cada vez más cerca de P1, de modo que la aceleración media se calcule en intervalos cada vez más cortos. La aceleración instantánea es el límite de la aceleración media conforme el intervalo de tiempo se acerca a cero. En el lenguaje del cálculo, la aceleración instantánea es la tasa instantánea de cambio de la velocidad con el tiempo. Así:

$a_{x} = \operatorname{}{\frac{v_{x}}{t} = \frac{dv_{x}}{\text{dt}}}$

Movimiento rectilíneo con aceleración Constante

Es el movimiento en donde la velocidad experimenta cambios iguales en cada unidad de tiempo. Permaneciendo constante el valor de la aceleración.

La aceleración afecta a la velocidad haciendo que los incrementos sean uniformes y se vaya aumentando o disminuyendo uniformemente.

Se considera una aceleración positiva cuando la velocidad se incrementa y se considera aceleración negativa cuando la velocidad disminuye uniformemente como cuando un auto aplica los frenos.

Este movimiento se rige por las siguientes expresiones, donde se encuentra la ley de velocidades, aceleración media, ley de posiciones, velocidad y desplazamiento.

Ley de velocidades:

$v = v_{0} + at$

Aceleración medio:

$a_{m} = \frac{v}{t} = \frac{v - v_{0}}{t - t_{0}}$

Ley de posiciones:

$d = d_{0} + v_{0}t + \frac{1}{2}at^{2}$

Velocidad y desplazamiento:

$v^{2} = v_{0}^{2} + 2ad$ $d = \left( \frac{v + v_{0}}{2} \right)t$

Ejemplo:

Un automóvil de carreras partió del reposo con una aceleración de 6 m/s2, ¿Cuál será el valor de su velocidad (rapidez) después de 10s? El automóvil se mueve en una carretera recta.

Solución:

$v_{0} = 0\ (reposo)$ $a = 6\frac{m}{s^{2}}$ $t = 10s$ $v = ?$

Formula:

$v = v_{0} + at$ $v = 0 + 6\frac{m}{s^{2}}(10s)$ $v = 60\frac{m}{s}$

Representación grafica

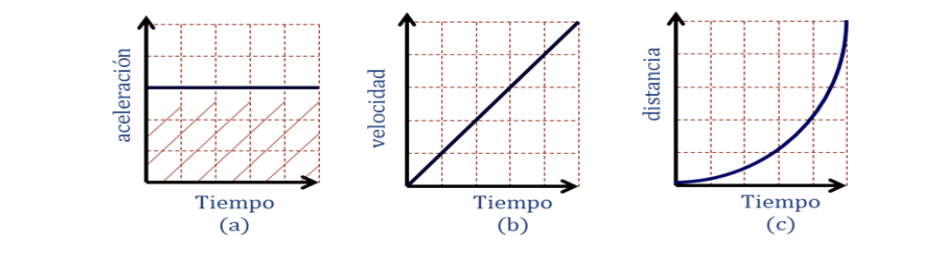
Caída libre

Un cuerpo en caída libre es definido como un cuerpo que se mueve a partir del reposo bajo la acción de la gravedad en un lugar en donde la resistencia del aire es despreciable.

Tiro Vertical: es el movimiento que describe un cuerpo cuando se lanza verticalmente hacia arriba.

Para la solución de estos movimientos utilizaremos las mismas ecuaciones del MRUA, tomando como aceleración a la gravedad de la tierra, la cual la representamos con la letra “g”. La gravedad al ser aceleración tiene un valor vectorial dirigido al centro de la tierra y su magnitud es:

$g = 9.8\frac{m}{s^{2}}$

Para el tiro vertical la gravedad tiene signo negativo si tomamos un sistema de referencia dirigido hacia arriba y la velocidad inicial será positiva.

En la caída libre la velocidad es negativa y la gravedad no cambia de signo si tomamos el mismo marco de referencia, o sea, hacia arriba. Sin embargo, se acostumbra cambiar el sistema de referencia dirigiéndolo hacia abajo, por lo que la velocidad y la gravedad ahora serán positivas.

Para estos dos movimientos debemos considerar que el tiempo que tarda en subir un objeto será igual al que utilice para bajar al mismo punto, por lo que la velocidad con que sale disparado dicho objeto será la misma con la que regrese, siempre y cuando estos puntos se encuentren a la misma altura.

$v_{f} = v_{0} + gt$ $h = v_{0}t + \frac{1}{2}gt^{2}$ $v_{f}^{2} = v_{0}^{2} + 2gh$

Ejemplo:

Una persona se cae de una tabla que cruza por encima de un arroyo y golpea el agua 1.2s después ¿Cuál es la altura de la tabla sobre el arroyo?

Solución:

$d = \frac{1}{2}gt^{2}$

Considerando

$g = 9.8\frac{m}{s^{2}}$ $t = 1.2s$

La altura se obtiene

$d = \ \frac{1}{2}\left( 9.8\frac{m}{s^{2}} \right)\left( 1.2s \right)^{2}$ $d = 7.05m$

Docente de Física 1 y TICs, Ing. en Computación egresado de la UNAM