Conceptos básicos de mecánica.

La mecánica es la parte de la física que estudia el movimiento y los casos de reposo. La mecánica se divide para su estudio en cinemática y dinámica.

La cinemática es la parte de la mecánica que permite conocer la posición, velocidad y aceleración que tiene un cuerpo que está en movimiento, sin considerar la causa que provoca el movimiento.

Las características del movimiento de un cuerpo son: trayectoria, desplazamiento, velocidad y aceleración en función del tiempo.

La dinámica es la parte de la mecánica que estudia el movimiento de los cuerpos atendiendo a las causas que lo producen. Estudia conceptos como fuerza, masa, energía, trabajo y potencia.

Magnitudes Escalares y Vectoriales

Algunas cantidades como el tiempo, la temperatura, la masa, las identificamos únicamente con un número y una unidad (magnitud) sin preocuparnos por nada más. Otras sin embargo tienen una dirección, es decir que no pueden ser descritas por un solo número, por lo que se requiere además que se indique hacia donde está dirigida esa cantidad.

Llamamos magnitud escalar, o simplemente escalar, a toda magnitud que puede expresarse simplemente con un único número. Por ejemplo, el peso o la altura de una persona es una magnitud escalar.

Las magnitudes escalares se pueden sumar o restar aplicando las reglas usuales del álgebra, con la condición de que presenten las mismas unidades. Por ejemplo:

Para multiplicar o dividir estas magnitudes no se requiere que presenten la misma unidad. Ejemplo:

Se denomina magnitud vectorial o vector a aquella medida para la cual necesitamos dar “algo más que un solo número”. Por ejemplo, para saber la velocidad del viento además de su intensidad, es decir, tantos kilómetros por hora, se requiere conocer su dirección y sentido, y así saber si viene del norte hacia el sur, etc. Este tipo de magnitudes se denominan vectores.

Las cantidades vectoriales se representan con vectores. Para la suma de estas cantidades se debe emplear algún método gráfico o analítico.

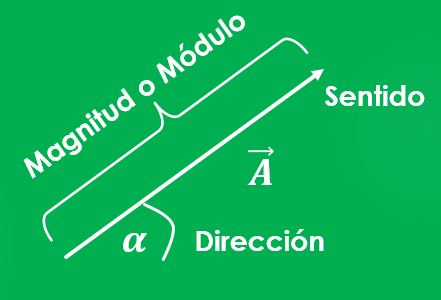
Vector: representación de una magnitud física que tiene un origen, magnitud, dirección y sentido. Se representa con una letra mayúscula A o con una flecha encima de A.

Un vector tiene las siguientes características:

Magnitud: Es la medida o tamaño del vector y se obtiene con la siguiente expresión:

Dirección: Es el ángulo que forma el vector con la horizontal y se determina con:

Sentido: Esta dado por los signos de las coordenadas del vector.

Características de un vector

Las cantidades vectoriales se representan por medio de un vector.

Un vector se define como un ente matemático que consta de: origen y extremo, dirección, sentido y magnitud o modulo.

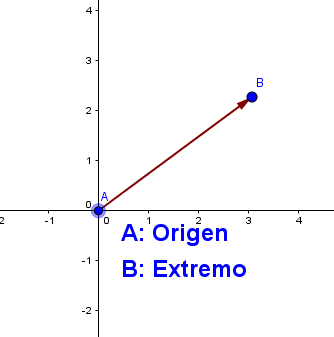
Origen y extremo. El origen, también denominado punto de aplicación, es el punto exacto sobre el que actúa el vector. El extremo es el punto donde finaliza el vector.

Dirección. Esta dada por la orientación en el espacio de la recta que lo contiene. Esto se logra indicado el ángulo con respecto a un eje de referencia (por ejemplo, la horizontal, representada generalmente como eje X) y se le llama ángulo director.

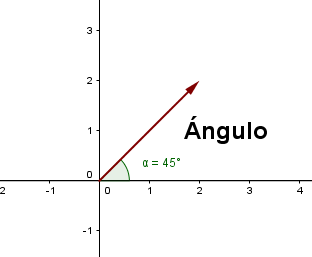
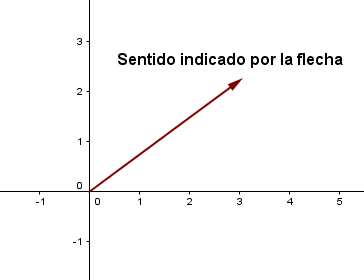
Sentido. Se Indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.

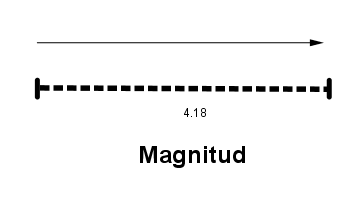
Magnitud o modulo. Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el modulo del vector debemos medir desde su origen hasta su extremo.

Para expresar gráficamente una magnitud vectorial se emplea una flecha (→) la cual, con su tamaño (longitud), nos indica su magnitud; la posición indica la dirección, es decir, su línea de acción; y hacia donde señale será el sentido.

Un vector siempre tendrá un origen o punto de aplicación y un extremo. Es necesario utilizar un marco de referencia para graficar un vector que generalmente es el plano cartesiano, aunque pueden utilizarse los puntos cardinales Norte, Sur, Este y Oeste e inclusive podríamos utilizar los términos arriba, abajo, derecha o izquierda.

Sistemas de Vectores

Al conjunto de vectores que actúan sobre un cuerpo en forma simultánea, se le llama sistema vectorial y cada uno de los vectores que lo forman, recibe el nombre de vector componente. Todos los vectores componentes pueden ser sustituidos por un vector único que cause el mismo efecto; al cual se le llama vector suma o vector resultante.

Los sistemas vectoriales se clasifican dependiendo de la dirección de los componentes en:

VECTORES COLINEALES: Son aquellos que se encuentran actuando sobre una misma línea de acción (dirección); dicho vectores pueden actuar en el mismo sentido o sentido contrario. La magnitud del vector resultante es la suma algebraica de los vectores componentes, con la misma dirección y sentido cuando el sentido de ambas es el mismo, pero cuando son de sentido opuesto la resultante tendrá el sentido de la mayor (numéricamente).

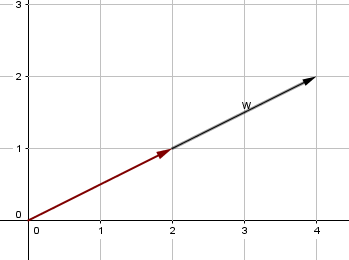
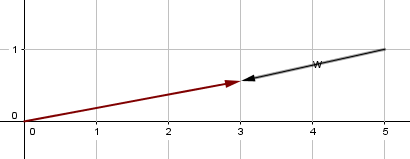
SISTEMA DE VECTORES PARALELOS: En este tipo de sistema de vectores componentes se encuentra actuando en la misma dirección y con sentido igual u opuesto, sin embargo, su punto de aplicación no está ubicado en la misma línea de acción sino en una línea paralela y aunque el vector resultante tiene la magnitud, dirección y sentido al igual que los colineales, el punto de aplicación cambia.

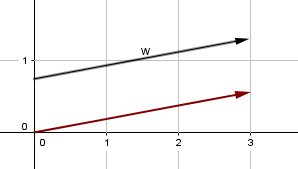
VECTORES CONCURRENTES: La mayor parte de los vectores tienen la propiedad de cambiar su punto de aplicación a lo largo de la misma dirección, sin perder sus propiedades. Esta propiedad permite desplazar a un vector sobre su línea de acción sin que se alteren sus efectos.

Presentación