¿Sabías que puedes navegar las publicaciones deslizando a la izquierda y la derecha?
Medición
14 Feb 2018
. category:
.
Método Científico
La ciencia en ningún momento pretende ser innegable o totalmente absoluta sino por el contrario se encuentra abierta a cualquier cambio o corrección, por lo que todas las ideas, hipótesis o teorías están sujetas a revisión e inclusive a una modificación parcial o total si así lo ameritase.
Para que sea posible la formulación de nuevas teorías, principios o leyes, e incluso para la modificación de las ya existentes, en cada ciencia, es necesario recurrir a un conjunto de procedimientos sistemáticos, los cuales se integran en el llamado método científico.
Teoría: Esquema que se compone como una explicación de un fenómeno o hecho a partir del cual se fundamenta un conocimiento o conjunto de conocimientos.
Fenómeno: Cambios espontáneos que suceden en la naturaleza. Los cambios pueden ser inducidos con el fin de ser estudiados.
El método científico: es un conjunto de reglas o normas para llevar a cabo una investigación, de tal forma que ésta sea lo más objetiva posible.
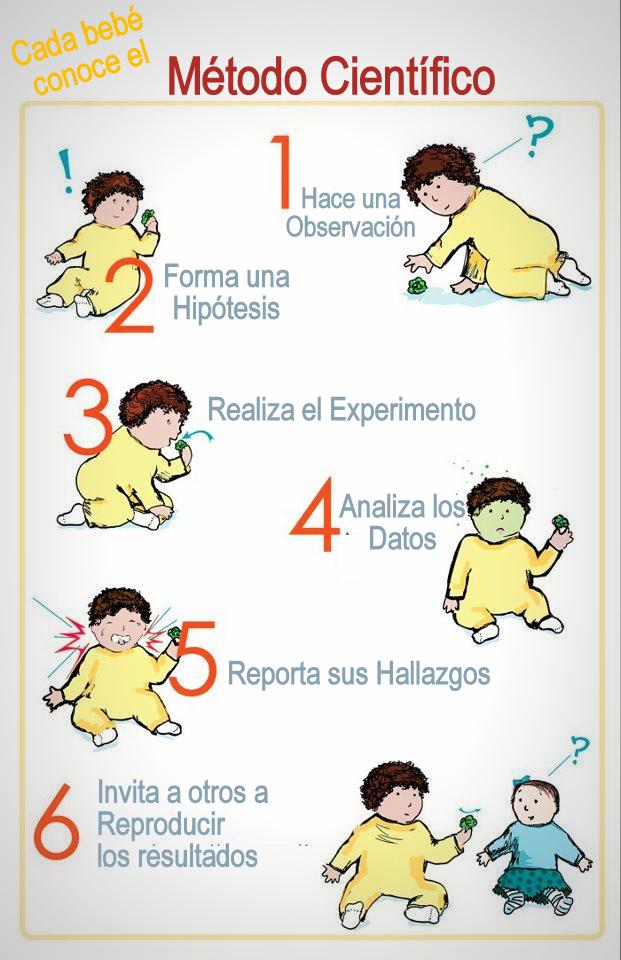
Es el conjunto de procedimientos que sigue la ciencia para obtener un conocimiento sobre la naturaleza. Consta de ciertos pasos recomendables, que permiten al investigador la posibilidad de explicar un fenómeno o suceso. Los pasos simplificados del método científico son:
1.Observación:
Consiste en aplicar nuestros sentidos a un fenómeno o aspecto del universo para recopilar información.
Por ejemplo: Observamos que un plumón cae más rápido que una hoja de papel abierta.
2.Planteamiento del problema:
Definir y delimitar, a partir de la observación, la problemática a la cual se le quiere dar solución o sobre la cual se quiere ampliar el conocimiento.
Ejemplo: Queremos demostrar que la rapidez con la que caen los objetos depende de su masa, puesto que, si dejamos caer la hoja de papel abierta y el plumón desde una misma altura cae primero el plumón y si medimos la masa de ambos encontramos que la del plumón es mayor.
3.Formulación de hipótesis:
Se elaboran las posibles explicaciones o soluciones para el fenómeno. Se utiliza la hipótesis para predecir al fenómeno.
Ejemplo: Caen con mayor rapidez los cuerpos que poseen mayor masa.
4.Experimentación:
Se trata de repetir el fenómeno para poner a prueba las hipótesis.
Ejemplo: Si lanzamos el plumón junto con una hoja arrugada y hecha bola, resulta que caen prácticamente al mismo tiempo. Si lanzamos ahora, una hoja de papel arrugada y otra sin arrugar desde una misma altura observamos que cae primero la arrugada aunque, como ya sabemos, poseen la misma masa.
5.Comprobación o análisis de resultados:
Consiste en comprobar con los resultados de la experimentación que la hipótesis es cierta, sin embargo, si no se encuentra una consistencia entre lo observado y la experimentación se formulan nuevas hipótesis o se mejora la anterior regresando a los pasos 3 y 4 hasta que no existan discrepancias entre ellas. Cuando se obtiene gran consistencia en este proceso se llega a una teoría o ley, que es un marco de referencia que sirve para explicar fenómenos.
Ejemplo: Podemos concluir, de acuerdo con la experimentación, que la masa prácticamente no determina que un objeto caiga más rápido que otro, es decir, nuestra hipótesis es incorrecta.
Medición
Para comprender y estudiar la naturaleza que le rodeaba, el hombre utilizó sus sentidos: el tacto, la vista, el gusto, etc., pero como éstos son limitados (por ejemplo no percibían el mundo microscópico) o distorsionaban o deformaban la realidad, como los espejismos, la sensación de caliente y frío, etc., tuvo que inventar aparatos para ampliar sus sentidos; así desarrolló instrumentos de medición, los cuales le ayudaron a percibir con mayor confiabilidad y claridad el mundo material que le rodeaba.
Con el paso de los años, la humanidad comprendió que para entender la naturaleza y explicarla, así como los fenómenos que en ella sucedían, eran necesarias la observación y la experimentación y con esto el hombre tubo la necesidad de medir, es decir, saber cuál es la magnitud de un objeto comparándolo con otro de la misma especie que le sirva de base o patrón.
Para la física y la química, en su calidad de ciencias experimentales, la medida constituye una operación fundamental. Sus descripciones del mundo físico se refieren a magnitudes o propiedades medibles.
Las unidades, como cantidades de referencia a efectos de comparación, forman parte de los resultados de las medidas. Cada dato experimental se acompaña de su error o, al menos, se escriben sus cifras de tal modo que reflejen la precisión de la correspondiente medida.
Medir: es comparar una magnitud con otra de la misma especie, que de manera arbitraria o convencional se toma como base, unidad o patrón de medida.
Al medir siempre intervienen tres aspectos:
Lo que se mide.
El aparato o instrumento de medición.
Las unidades de medida del sistema establecido.
Las mediciones pueden hacerse de forma directa o indirecta. Lo hacemos de manera directa cuando medimos la altura de una persona con una cinta métrica, cuando tomamos el tiempo que alguien dura sumergido debajo del agua o al llenar una taza o una cuchara de un ingrediente al momento de seguir una receta. Medimos de manera indirecta cuando tomamos la temperatura de una persona con fiebre, cuando calculamos la velocidad de un vehículo o la distancia entre la tierra y la luna, etc.
Las mediciones exactas y confiables requieren unidades inmutables que los observadores puedan volver a utilizar en distintos lugares. El sistema de unidades empleado por los científicos e ingenieros en todo el mundo se denomina comúnmente “sistema métrico” aunque, desde 1960, su nombre oficial es Sistema Internacional,
Con el paso de los años, las definiciones de las unidades básicas del sistema métrico han evolucionado. Cuando la Academia Francesa de Ciencias estableció el sistema en 1791, el metro se definió como una diezmillonésima parte de la distancia entre el Polo Norte y el ecuador. El segundo se definió como el tiempo que tarda un péndulo de 1 m de largo en oscilar de un lado a otro. Estas definiciones eran poco prácticas y difíciles de duplicar con precisión, por lo que se han refinado por acuerdo internacional.
Sistemas de unidades
Las civilizaciones antiguas tenían cada una su propia forma de medir las cosas. Los egipcios usaban la brazada o braza, cuya longitud equivalía a las dimensiones de un hombre con los brazos abiertos.
También se utilizaban otras medidas del cuerpo humano como el pie, el codo (distancia desde el codo hasta la punta de los dedos), el palmo (la longitud de cuatro dedos juntos), la pulgada (la longitud del dedo pulgar).
Anteriormente, las unidades de medida variaban de un país a otro, no existía un sistema unificado y esto limitaba la relación entre los países y el desarrollo global de las ciencias.
Por tal motivo, en 1795 se llevó a cabo la Convención Mundial de las Ciencias en París, Francia, y se estableció un sistema universal de medidas, llamado sistema métrico decimal.
En 1875 se realizó en París la Convención del Metro, teniendo como resultado el compromiso de 18 naciones para adoptar el uso del sistema métrico decimal, excepto Inglaterra, que no acudió a esta reunión y se negó a emplear estas unidades.
El sistema métrico decimal se adoptó internacionalmente en la Conferencia General de Pesos y Medidas (CGPM) de 1889 y dio como resultado el Sistema Internacional de Medidas, en 1960 se sustituyó por otro más preciso, el Sistema Internacional de Unidades (SI), que se utiliza actualmente en 95% de la población mundial.
Magnitud: es todo aquello que puede ser medido, como el tiempo, la longitud, la masa, el área, el volumen, la densidad, la fuerza, etc. y se representa con un número y una unidad.
Magnitudes fundamentales: son aquellas que se definen con un número y una unidad y sirven de base para obtener las demás magnitudes utilizadas en la física.
Los diferentes sistemas de unidades se describen a continuación:
A) Sistema métrico decimal.
Es el primer sistema de unidades que hubo en el mundo, implantado en 1795 como resultado de la Convención Mundial de Ciencia celebrada en París Francia. Tiene una división decimal y sus unidades fundamentales son el metro, el kilogramo y el litro.
Para definir las unidades fundamentales utiliza datos de carácter general como las dimensiones de la tierra y la densidad del agua.
Una ventaja importante del sistema métrico decimal fue su división decimal ya que hace uso de prefijos como deci, ceti, mili.
B) Sistema cegesimal (cgs).
El sistema cegesimal de unidades o sistema cgs, es un sistema de unidades basado en el centímetro, gramo y segundo. Su nombre deriva de las iniciales de estas tres unidades. Fue propuesto en 1881 en el congreso Internacional de los Electricistas realizado en París, Francia, propuesto por el Físico Alemán Karl Gauss.
C) Sistema MKS o absoluto.
En 1935, en el Congreso Internacional de los Electricistas celebrado en Brucelas, Bélgica, el ingeniero italiano, Giovani Giorgi propone y logra que se acepte su sistema, también llamado absoluto, pues como magnitud fundamental se habla de la masa y no del peso de los cuerpos. Recibe el nombre de MKS, cuyas iniciales corresponden al metro, kilogramo y segundo como unidades de longitud, masa y tiempo.
D) Sistema Inglés:
También llamado sistema convencional de unidades, aún se emplea en Estados Unidos a pesar de la aceptación del sistema internacional de unidades por el resto del mundo. En este sistema las unidades de longitud, masa y tiempo son: el pie, el slug y el segundo.
| Cantidad o magnitud | M.K.S. | C.G.S. | F.P.S. |
|---|---|---|---|
| Longitud (L) | Metro (m) | Centímetro (cm) | Pie (ft) |
| Masa (M) | Kilogramo(kg) | Gramo (g) | Libra (lb) |
| Tiempo (T) | Segundo (s) | Segundo (s) | Segundo (s) |
| Fuerza(F) | Newton (N) | Dina | Poundal (Pdl) |
E) Sistema Internacional (SI):
En 1960 científicos y técnicos de todo el mundo se reunieron en ginebra Suiza y acordaron adoptar el llamado Sistema Internacional de Unidades, el cual se basa en el MKS. Tiene como magnitudes y unidades fundamentales al metro (m) para longitud, al kilogramo (Kg) para masa, al segundo (s) para tiempo, al grado kelvin (K) para temperatura, al ampere (A) para intensidad de la corriente, la candela (cd) para la intensidad luminosa y el mol para cantidad de sustancia.
Se conocen como magnitudes fundamentales aquellas que no se definen en función de otras magnitudes físicas y por lo tanto sirven de base para obtener las demás magnitudes usadas en la Física.
Existen otras magnitudes llamadas derivadas y son aquellas que resultan de multiplicar o dividir las magnitudes fundamentales, entre ellas están: área, volumen, velocidad, aceleración, fuerza, trabajo, presión, potencia, entre otras.
| Magnitud | Nombre | Símbolo |
|---|---|---|
| Longitud | Metro | M |
| Masa | Kilogramo | Kg |
| Tiempo | Segundo | S |
| Intensidad de corriente eléctrica | Amperio | A |
| Temperatura termodinámica | Kelvin | K |
| Cantidad de sustancia | Mol | Mol |
| Intensidad luminosa | Candela | Cd |
Kilogramo: la masa de un cilindro fabricado con una aleación de platino-iridio.
Metro: es la distancia recorrida por la luz en el vacío durante un intervalo de 1/299792458 m/s
Segundo: es el tiempo que requiere un átomo de cesio 133 para realizar 9192631770 vibraciones.
Kelvin: se define como la fracción 1/273.16 de la temperatura triple del agua.
Ampere: es la intensidad de corriente eléctrica constante, entre dos conductores paralelos, de longitud infinita, separados a una distancia de un metro y situados en el vacío, produce entre dichos conductores una fuerza de 2x10^-7.
Mol: es la cantidad de sustancia de un sistema que contiene un nuero de entidades elementales equivalente a la cantidad de átomos que hay en 0.012kg de carbono 12.
Candela: es la cantidad luminosa en una dirección dada de una fuente que emite una radiación monocromática de frecuencia 540x10^12 hertz y cuya intensidad energética en esa dirección es 1/683 watt por esterradían.
Unidades SI derivadas
| Magnitud | Nombre | Símbolo |
|---|---|---|
| Área, superficie | Metro cuadrado | m^2 |
| Volumen | Metro cúbico | m^3 |
| Velocidad | Metro por segundo | m/s |
| Aceleración | Metro por segundo cuadrado | m/s^2 |
| Número de ondas | Metro a la potencia menos uno | m^-1 |
| Densidad, masa en volumen | Kilogramo por metro cúbico | kg/m^3 |
| Densidad superficial | Kilogramo por metro cuadrado | kg/m^2 |
| Volumen específico | Metro cúbico por kilogramo | m3/kg |
| Densidad de corriente | Amperio por metro cuadrado | A/m^2 |
| Concentración de cantidad de sustancia, concentración | Mol por metro cúbico. | mol/m^3 |
| Concentración másica | Kilogramo por metro cúbico | kg/m^3 |
| Luminancia | Candela por metro cuadrado. | cd/m^2 |
| Índice de refracción | Uno | 1 |
| Permeabilidad relativa | Uno | 1 |
Prefijos de las Unidades del SI
Conversión de unidades
En virtud de la existencia de un gran número de sistemas, es necesario convertir unidades de un sistema a otro, teniendo para ello en consideración las equivalencias.
Usamos ecuaciones para expresar las relaciones entre cantidades físicas representadas por símbolos algebraicos. Cada símbolo algebraico denota siempre tanto un número como una unidad. Por ejemplo, d podría representar una distancia de 10 m, t un tiempo de 5 s y v una rapidez de 2 m>s.
Toda ecuación siempre debe ser dimensionalmente consistente. No podemos sumar manzanas y automóviles; sólo podemos sumar o igualar dos términos si tienen las mismas unidades. Por ejemplo, si un cuerpo que viaja con rapidez constante v recorre una distancia d en un tiempo t, estas cantidades están relacionadas por la ecuación d 5 vt.
Si d se mide en metros, entonces el producto vt también debe expresarse en metros. Con los números anteriores como ejemplo, escribimos Como la unidad 1>s del lado derecho de la ecuación cancela la unidad s, el producto está en metros, como debe ser.
En los cálculos, las unidades se tratan igual que los símbolos algebraicos en cuanto a la multiplicación y la división.
Cuando un problema requiere de cálculos con números y unidades, siempre escriba los números con las unidades correctas durante todo el cálculo, como en el ejemplo. Esto es muy útil, pues ayuda a verificar los cálculos.
Si en algún momento una ecuación o expresión tiene unidades inconsistentes, es indicador de que hay un error en alguna parte.
Para poder llevar a cabo las conversiones es necesario realizar los siguientes pasos:
Paso 1.-
Se escribe la cantidad con la unidad de medida que se desea convertir:
Paso 2.-
Se pone el signo de multiplicación y una raya de quebrado, ambos signos nos indicarán que haremos dos operaciones, una de multiplicación y una de división.
Paso 3.-
Se hace uso de las equivalencias entre las unidades involucradas, la que se desea convertir y la que se desea obtener, y con ello se encuentra el factor de conversión.
Por ejemplo nosotros deseamos convertir 2m a cm, entonces:
Paso 4.-
Conociendo los factores de conversión, se colocan de la siguiente manera:
De esta forma se pueden eliminar los metros.
Ejemplo:
Si un libro tiene una longitud de 21.6 cm, ¿cómo se expresa en metros esta
longitud?
Solución
Sabemos que la relación entre un metro y un centímetro es 1 m = 100 cm.
Para realizar la conversión siempre comenzamos poniendo la cantidad que queremos convertir en forma de fracción (con 1 como denominador), y enseguida se multiplica por la relación, poniendo debajo la cantidad que queremos eliminar y se realiza la multiplicación de fracciones (numerador por numerador y denominador por denominador), eliminado las unidades iguales:
Ejemplo:
Si se compra en la pollería ¾ de kg de pollo, ¿a cuántos gramos equivalen?
Solución
Primero se convierte la fracción a decimal dividiendo, y lo que resulta es 0.75 kg
Sabemos que 1 kg = 1000 g
Por lo tanto, los o 0.75 kg equivalen a 750 g de pollo.
Ejemplo:
¿Cuántos segundos equivalen a 27 minutos?
Solución
Sabemos que la relación entre un minuto y los segundos es; 1 min = 60 s
Por lo tanto, 27 minutos equivalen a 1,620 s
Ejemplo:
Un ciclista viaja a una velocidad de 28 km/h. ¿A cuántos m/s viaja el ciclista?
Solución
Sabemos que 1 h = 60 min y que 1min = 60 s, por lo que si multiplicamos ambas cantidades obtenemos que 1 h = 3,600 s.
Recuerda que se multiplican todos los numeradores y el resultado se divide entre la multiplicación de los denominadores
Por lo tanto, 28 km/h equivalen a una velocidad de 7.77 m/s.
Tabla de conversión de unidades
| 1 milla= 1.609 km |
| 1 libra= 454 g |
| 1 kg = 2.2 libras |
| 1 cm3 = 1 ml |
| 1 litro = 1 000 m^3 |
| 1 litro=1 dm^3 |
| 1 galón = 3.785 litros |
| 1 ton = 1000 kg |
| 1 m = 100 cm |
| 1 m = 1000 mm |
| 1 cm = 10 mm |
| 1 km = 1 000 m |
| 1 m = 3.28 pies |
| 1 m = 1.093 yardas |
| 1 pie= 30.48 cm |
| 1 pie= 12 pulgadas |
| 1 pulg = 2.54 cm |
Análisis de errores
La física se fundamenta en la determinación cuantitativa de las magnitudes pertinentes de los fenómenos que estudia, medir implica comparar con una unidad patrón. Las medidas en ocasiones no permiten obtener el verdadero valor de las magnitudes que se miden. En algunos aparatos se presentan imperfecciones y en otras nuestros sentidos cometen equivocaciones. Se tiene que muchas medidas son inciertas o tienen un cierto grado de incertidumbre. Al expresar el resultado de una medida pueden especificarse tres elementos: número, unidad e incertidumbre. Se distinguen dos tipos de errores: errores sistemáticos y accidentales.
- Errores sistemáticos. Surgen al emplear un método inadecuado, un instrumento defectuoso o por usarlo en condiciones imprevistas para su uso. Al no realizarse las lecturas correctamente o bien al no tener un rango de precisión adecuado el instrumento de medición.
- Errores accidentales. Son incertidumbres debidas a numerosas causas incontrolables e imprevistas que dan lugar a resultados distintos cuando se repite la medida.
El error obtenido en una medición puede expresarse en dos formas:
Error absoluto: es la diferencia del valor obtenido en la medición menos el valor promedio de las mediciones.
Error relativo: se obtiene dividiendo el error absoluto entre el valor promedio de las mediciones. Mediante éste se puede saber la calidad de la medición.
El promedio de los errores con respecto al promedio de las medidas se representa por la desviación media.
Utilizaremos las siguientes fórmulas:
- Valor promedio:
- Error absoluto:
- Desviación media:
- Error relativo:
- Error porcentual:
Ejemplo:
Al medir 6 veces la longitud de un palo de escoba se obtuvieron las siguientes medidas:
1.56 m, 1.58 m, 1,55 m, 1.59 m, 1.57 m, 1.60 m
Determina:
a) El valor más probable de la longitud del palo de escoba.
Se procede a calcular la media o promedio.
$$m = \frac{1.56 + 1.58 + 1.55 + 1.59 + 1.57. + 1.60}{6} = \frac{9.45}{6} = 1.575$$Por tanto, el valor más probable redondeado a 2 cifras (porque las mediciones se hicieron con 2 cifras) es m = 1.58 m (recuerda que en el redondeo si la última cifra significativa es 5 o mayor, la cifra anterior sube; si es 4 o menor se queda igual).
b) El error absoluto de la medida.
Se determinan las desviaciones absolutas de cada medida (recuerda que las barras horizontales \| \| significan valor absoluto, que es siempre el valor positivo del resultado).
Por lo tanto, el valor más probable redondeado a 2 cifras (porque las mediciones se hicieron con 2 cifras) es Δm = 0.02 m
c) La longitud del palo de escoba se debe expresar así:
$$M = m \pm \Delta m$$ $$M = 1.58 \pm 0.02m$$Lo que indica que estará entre 1.58 – 0.02 = 1.56 y 1.58 + 0.02 = 1.60 m, es decir, la medida del palo de escoba estará entre 1.56 y 1.60 m
d) El error relativo de la medida
Se divide el error absoluto entre el valor más probable
$$E_{R} = \frac{\Delta m}{m} = \frac{0.02}{1.58} = 0.0126$$ $$E_{R} = 0.0126$$e) El error porcentual
Se multiplica el error relativo por 100
$$E_{P} = E_{R} \times 100$$ $$E_{P} = 0.0126 \times 100 = 1.26$$ $$E_{P} = 1.26\%$$Lo que indica que hay una variación de 1.26% entre las medidas realizadas
