¿Sabías que puedes navegar las publicaciones deslizando a la izquierda y la derecha?

Suma de vectores - Métodos analíticos

18 Feb 2020 . category: 1erPeriodoFísica .
#método #analítico #vectores #senos #cosenos #Pitágoras #triangulo

Presentación electronica

Métodos analíticos

Estos métodos sirven para determinar la magnitud y la dirección de la resultante, utilizando leyes o teoremas matemáticas; son más exactos y precisos que los métodos gráficos ya que se realizan a base de cálculos.

Método de Pitágoras

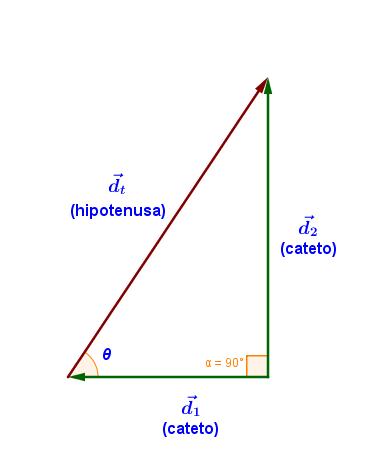
Este método se basa en el teorema de Pitágoras y nos sirve para sumar dos vectores cuando forman un ángulo de 90° entre sí. El valor de la resultante se calcula por medio del teorema de Pitágoras, mientras que la dirección o ángulo de la resultante se determina por medio de cualquier función trigonométrica, aunque lo más frecuente es la utilización de la tangente.

El vector resultante se dibuja entre el origen del primer vector y el extremo del segundo vector, este será la hipotenusa del triángulo rectángulo formado por los tres vectores.

La magnitud del vector resultante se puede determinar mediante el teorema de Pitágoras que relaciona las magnitudes de los dos primeros vectores $\overrightarrow{d_{1}}$ y $\overrightarrow{d_{2}}$ (Catetos) con la magnitud del vector resultante $\overrightarrow{d_{t}}$ (Hipotenusa) por la siguiente ecuación:

$d_{t} = \sqrt{d_{1}^{2} + d_{2}^{2}}$

Para determinar la dirección del vector resultante, se puede emplear el transportador para medir el ángulo que forma el vector resultante con respecto a uno de los vectores sumados y en forma matemática mediante la función tangente:

$\theta = \tan^{- 1}\left( \frac{\text{cateto\ opuesto}}{\text{cateto\ adyacente}} \right)$

O bien:

$\theta = \tan^{- 1}\left( \frac{d_{1}}{d_{2}} \right)$

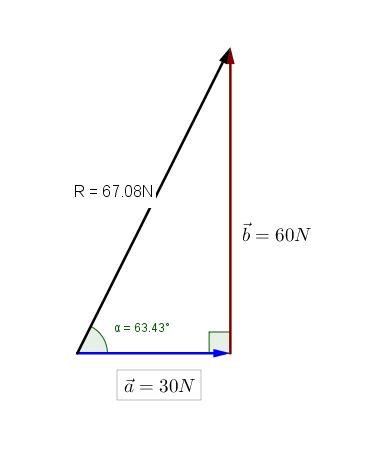
Ejemplo:

Determinar:

a) la gráfica

b) la resultante

c) el ángulo de la resultante

De la suma de los siguientes vectores:

b = 30 N a 0º

a = 60 N a 90º

Solución:

Método de la ley de cosenos y la ley de senos

En este método se emplea la ley de cosenos y la ley de senos para determinar la magnitud y dirección del vector resultante de dos vectores concurrentes cuando el ángulo entre ellos es diferente de 90°, aunque se puede usar este método cuando el ángulo es de 90°.

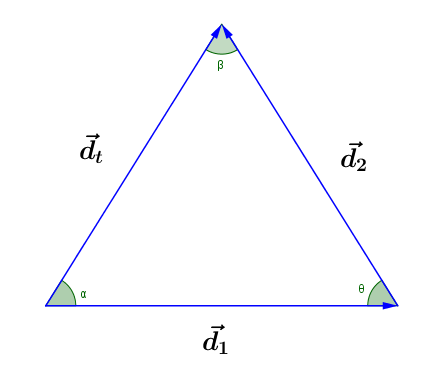
Ley de cosenos

La magnitud del vector resultante $\ \overrightarrow{d_{t}}$ se puede determinar por la ley de cosenos, al cual establece:

En un triángulo cualquiera, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos, menos el doble del producto de los mismos por el coseno del ángulo que forma entre sí.

Matemáticamente:

$(d_t^2 )=d_1^2+d_2^2-2d_1 d_2 \cos \Theta$ $d_{t} = \sqrt{d_{1}^{2} + d_{2}^{2} - 2d_{1}d_{2}\cos \Theta }$

Ley de senos

La dirección del vector resultante se puede determinar mediante la ley de senos, la cual establece:

En un triángulo cualquiera los lados son proporcionales al seno de los ángulos opuestos.

Matemáticamente:

$\frac{d_{1}}{\sin \beta } = \frac{d_{2}}{\sin \alpha } = \frac{d_{t}}{\sin \theta }$

Ejemplo:

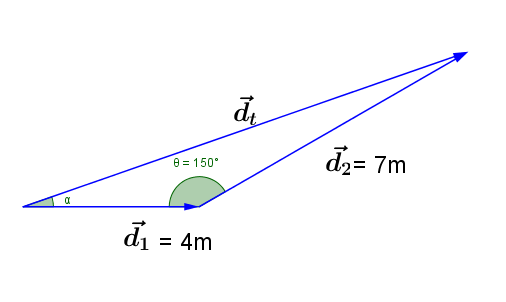
Determina el vector resultante del sistema de vectores mostrado en el siguiente esquema:

Solución:

$d_{1} = 4m$ $d_{2} = 7m$ $\theta = 150^{\circ}$

La magnitud se obtiene de:

$d_{t} = \sqrt{d_{1}^{2} + d_{2}^{2} - 2d_{1}d_{2}\cos \Theta }$

La dirección se obtiene de:

$\frac{d_{2}}{\text{sen}\ \alpha} = \ \frac{d_{t}}{\text{sen}\ \theta}$

Para la magnitud:

$d_{t} = \sqrt{4^{2} + 7^{2} - 2\left( 4 \right)\left( 7 \right)\cos{150^{\circ}}}$ $d_{t} = \sqrt{113.497}$ $d_{t} = 10.6m$

Para la dirección:

$\frac{7}{\text{sen}\ \alpha} = \ \frac{10.6}{\text{sen}\ 150^{\circ}}$ $\alpha = \operatorname{\left( \frac{7\ \sin 150^{\circ}}{10.6} \right) }$ $\alpha = 19.2^{\circ}$

Por tanto, el vector resultante es:

$\overrightarrow{d_{t}} = 10.6m\sphericalangle 19.2^{\circ}$

Componentes ortogonales de un vector

Un sistema de vectores puede sustituirse por otro equivalente que contenga un número mayor o menor de vectores que el sistema considerado. Si el sistema equivalente tiene un mayor número de vectores, el procedimiento se llama descomposición. Si tiene un número menor de vectores, el procedimiento se denomina composición.

El procedimiento para determinar la suma de vectores por el método de los componentes es el siguiente:

1.Se determina el componente horizontal y vertical de cada vector.

$V_{y} = V\ sen\theta$ $V_{x} = V\ cos\theta$

2.Se suman las componentes horizontales para obtener un vector en la dirección horizontal, denotado por Σx. Es importante mencionar que cada componente horizontal se multiplica por el coseno del ángulo, esto es:

$\sum{x} = \left( F_{1}x \right)\left( \cos\alpha \right) + \left( F_{2}x \right)\left( \cos\beta \right) + \left( F_{3}x \right)\left( \cos\gamma \right) + \ldots$

Hay que tomar en cuenta que si el vector está del lado derecho, se toma positivo, y si está del lado izquierdo se toma como negativo.

3.Se suman las componentes verticales para obtener un vector en la dirección vertical, denotado por Σy. Es importante mencionar que cada componente vertical se multiplica por el seno del ángulo, esto es:

$\sum{y} = \left( F_{1}y \right)\left( \operatorname{sen}\alpha \right) + \left( F_{2}y \right)\left( \operatorname{sen}\beta \right) + \left( F_{3}y \right)\left( \operatorname{sen}\gamma \right) + \ldots$

Hay que tomar en cuenta que si el vector está del lado superior, se toma positivo, y si está del lado inferior se toma como negativo.

4.Para encontrar analíticamente la magnitud de la resultante, se utiliza el Teorema de Pitágoras

$R = \sqrt{\left( \sum{x} \right)^{2} + \left( \sum{y} \right)^{2}}$

5.El ángulo se determina por

$\theta = tan^{-1}\left( \frac{\sum{y}}{\sum{x}} \right)$

Y se forma con respecto al eje x.

Ejemplo:

Encuentre las componentes de “x” y de “y” del siguiente vector fuerza:

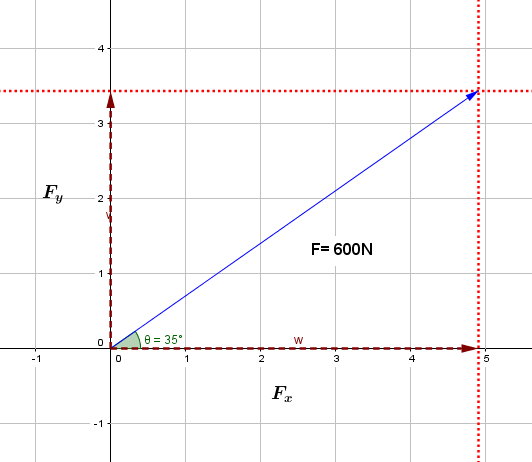
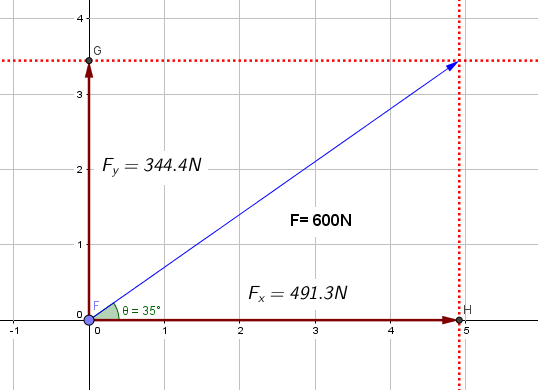
Solución:

Usamos directamente:

$V_{y} = V\ \sin \Theta$ $V_{x} = V\ \cos \Theta$ $V_{y} = (600N)\ sen(35)$ $V_{x} = (600)\ cos(35)$ $V_{y} = 344.146N \uparrow$ $V_{x} = 491.491N \rightarrow$

Ejemplo:

Calcular la fuerza resultante del siguiente sistema de vectores

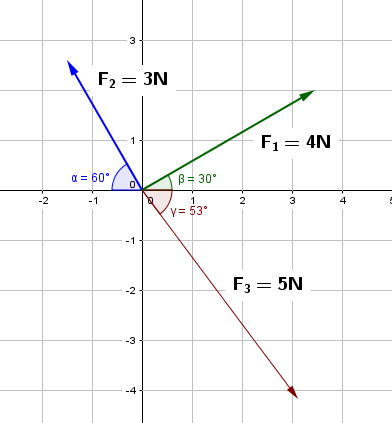
Solución:

Descompongamos cada una de las fuerzas apoyándonos de la siguiente tabla:

*El ángulo se mide a partir del eje x del primer cuadrante y será positivo en el sentido contrario a las manecillas del reloj.

Representemos ahora las sumatorias de fuerzas “x” y “y” en un plano cartesiano, nota que ambas son positivas:

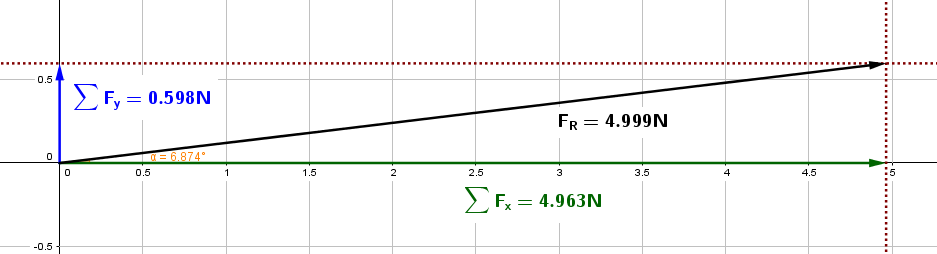
Calcular la fuerza resultante y su ángulo de inclinación:

$F_{R} = \sqrt{\left( 4.964N \right)^{2} + \left( 0.598N \right)^{2}}$ $F_{R} = 5N$ $\alpha = \tan^{- 1}\left( \frac{0.598}{4.964} \right)$ $\alpha = 6.87^{\circ}$

Version Antigua

Docente de Física 1 y TICs, Ing. en Computación egresado de la UNAM

Suma de vectores - Métodos analíticos

18 Feb 2020 . category: 1erPeriodoFísica . #método #analítico #vectores #senos #cosenos #Pitágoras #triangulo

Presentación electronica

Métodos analíticos

Método de Pitágoras

Método de la ley de cosenos y la ley de senos

Ley de cosenos

Ley de senos

Componentes ortogonales de un vector

18 Feb 2020 . category: 1erPeriodoFísica .
#método #analítico #vectores #senos #cosenos #Pitágoras #triangulo