Suma de vectores - Métodos gráficos

Presentación electronica

Pantalla completa

Suma de vectores

Sumar dos o más vectores es determinar su resultado o el efecto total que ejerce los vectores del sistema. Para determinar la resultante de un sistema de vectores concurrentes, se emplean diferentes métodos.

Suponga que una partícula sufre un desplazamiento, seguido por un segundo desplazamiento. El resultado final es el mismo que si la partícula hubiera partido del mismo punto y sufrido un solo desplazamiento como se muestra. Llamamos a suma vectorial, o resultante, de los desplazamientos y Expresamos esta relación simbólicamente como:

Antes de pasar a la aplicación de estos métodos es necesario tener en cuenta las siguientes consideraciones.

La convención de signos en el plano cartesiano es: para la “x”, positivo a la derecha y negativo a la izquierda; para la “y”, positivo arriba y negativo abajo.

Debemos usar una escala para representar la magnitud vectorial por medio de una flecha.

Otro concepto de importancia a considerar antes de aprender cada método es el Vector Resultante.

Vector Resultante: El vector resultante de un sistema de vectores, es un vector que produce el mismo efecto que todos los vectores que lo componen.

Métodos gráficos

Como su nombre lo indica, son métodos en los que para determinar el vector suma o resultante, se debe trazar gráficas de los vectores componentes, a escala y respetando sus direcciones. Tanto la magnitud como la dirección de la resultante se determinan por medición directa en la gráfica.

Para sumar vectores por el método del polígono se colocan los vectores consecutivamente respetando el origen y sus sentidos, el vector resultante se obtiene uniendo el origen del primer vector con el extremo final del último vector.

El método del paralelogramo es útil para sumar dos vectores concurrentes y basta con trazar líneas auxiliares paralelas a los vectores originales, para formar un paralelogramo: cada vector original se dibuja a escala, formando lados adyacentes a partir de las puntas de flechas que limitan a los vectores originales trazando líneas paralelas hasta que se interceptan, la resultante será la diagonal que une el punto de concurrencia de los vectores originales hasta el punto de intersección de las líneas auxiliares, interpretando la longitud con la escala de mediada utilizada.

Método del triangulo

Válido sólo para dos vectores concurrentes y coplanares. Los vectores se trasladan sin cambiar sus propiedades de tal forma que la punta de la flecha de uno se conecte con el origen del otro. El vector resultante se representa por la flecha que une la punta libre con el origen libre y entonces se forma un triángulo que se representa con la letra R.

Se mide la distancia entre el origen y la punta de la flecha de b y ésa es la medida del desplazamiento del vector resultante. La distancia recorrida se obtiene sumando los dos vectores.

Este método nos sirve para sumar dos vectores de acuerdo a las siguientes reglas:

1.Se traza el primer vector, respetando su dirección.

2.Al final del primero, se traza el segundo.

3.Se une el principio del primero con el final del segundo y esa será su resultante.

4.Se mide la magnitud y la dirección del vector resultante directamente en la gráfica, obteniéndose valores aproximados

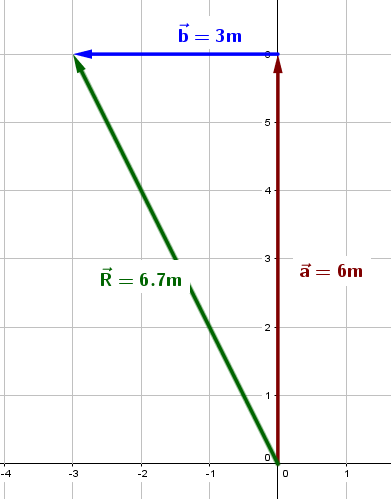
Ejemplo:

Una persona camina 6 m al norte y luego 3 m al oeste. ¿Cuál fue su desplazamiento y qué distancia recorrió?

Solución

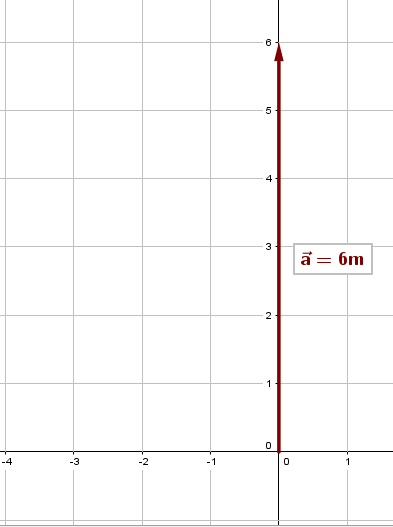
1.Se toma la escala 1 m = 1 cm

2.Se traza el desplazamiento del vector $\overrightarrow{a}$ hacia el norte (6 m = 6 cm) partiendo del origen.

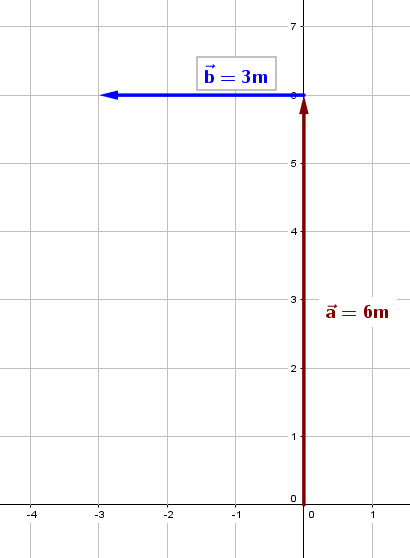
3.Se traza el desplazamiento del vector$\overrightarrow{b}$ al oeste (3 m = 3 cm) a partir de la punta de la flecha del vector $\overrightarrow{a}$.

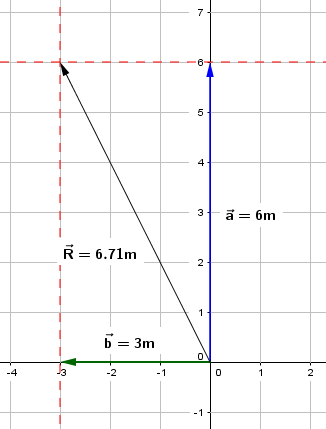
4.Se traza la resultante a partir del origen y hasta llegar a la punta de la flecha del vector $\overrightarrow{b}$, y se mide el vector resultante, con un desplazamiento de R = 6.7 cm o R = 6.7 m.

La distancia que recorrió esta persona fue de 6 m + 3 m = 9 m

Tambien puedes verlo en este link: Ejemplo

Método del Paralelogramo

Recibe también el nombre de método del rectángulo y sólo sirve para sumar dos vectores de acuerdo a las siguientes reglas.

1.Se traza dos vectores con un solo origen (deben de coincidir sus puntos de aplicación).

2.Al final de cada vector, se traza paralelas al otro vector.

3.Se une el origen con el punto donde se cruzan las paralelas y esa será resultante.

4.Se mide la magnitud y al dirección de la resultante directamente sobre la gráfica obtenido valores aproximados.

También lo puedes ver en este link: Ejemplo

Ejemplo:

Una persona camina 6 m al norte y luego 3 m al oeste. ¿Cuál fue su desplazamiento y qué distancia recorrió?

Solución

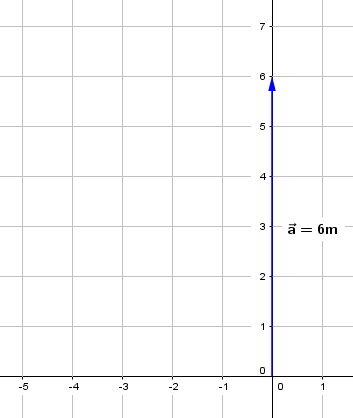
1.Se toma la escala 1 m = 1 cm

2.Se traza el desplazamiento del vector a hacia el norte (6 m = 6 cm) partiendo del origen.

3.Se traza el desplazamiento del vector b al oeste (3 m = 3 cm) a partir del origen.

4.Se trazan las dos paralelas de a y b.

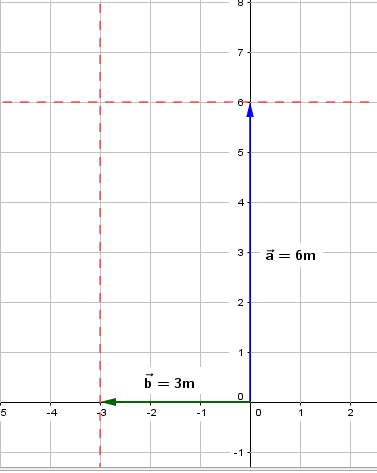
5.Se traza la resultante a partir del origen y hasta llegar a la intersección de las dos paralelas, y se mide el vector resultante, con un desplazamiento de R = 6.7 cm o R = 6.7 m.

La distancia que recorrió esta persona fue de 6 m + 3 m = 9 m

Método del polígono

Este método es simplemente la extensión del método del triángulo. Es decir, dibujan los vectores para colocar la “punta” del uno con el “origen” del otro y la resultante es el vector que cierra el polígono desde el “origen” libre hasta la “punta” libre. Nuevamente el orden en que se realice la suma no interesa, pues aunque el polígono resultante tiene forma diferente en cada caso, la resultante final conserva su magnitud, dirección y sentido.

Este método sirve para sumar 3 o más vectores y se considera como una extensión del método del triángulo. La resultante se obtiene de acuerdo al siguiente procedimiento:

1.Se traza el primer vector.

2.Al final del primero, se traza el segundo.

3.Al final del segundo, el tercero y así sucesivamente hasta que se agoten todos los vectores (no importa que se superpongan).

4.Se une el principio del primero con el final del último y esa será la resultante.

5.La magnitud y la dirección de la resultante, se miden directamente en la gráfica.

6.No importa el orden en que se toman los vectores, el resultado será el mismo.

Ejemplo:

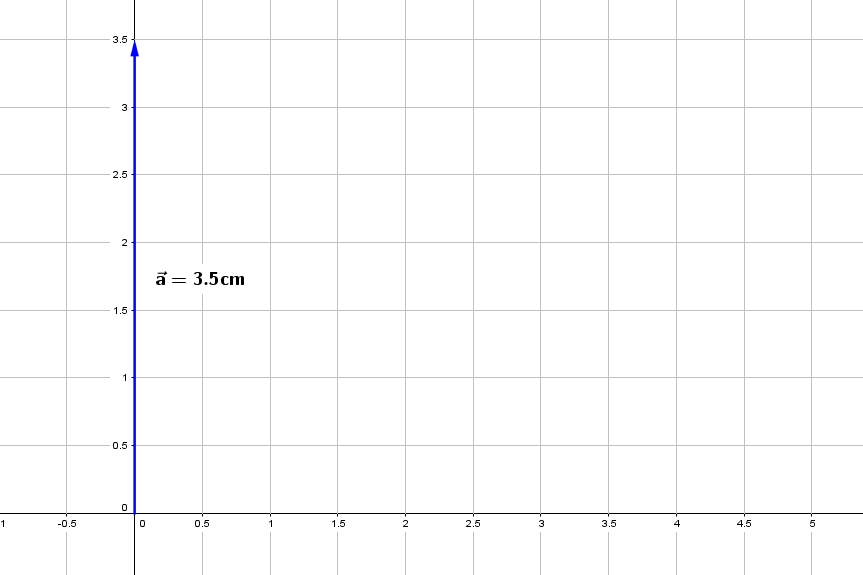
Una persona sale a correr desde su casa, primero 350 m al norte, luego 200 m al este, 150 m al sureste y por último 100 m al sur. ¿Cuál fue la distancia total recorrida y cuál fue su desplazamiento? Toma la escala 100 m = 1 cm.

Solución:

1.Se traza el vector $\overrightarrow{a}$ a partir del origen.

2.Se traza el vector $\overrightarrow{b}$ a partir de la punta del vector $\overrightarrow{a}$

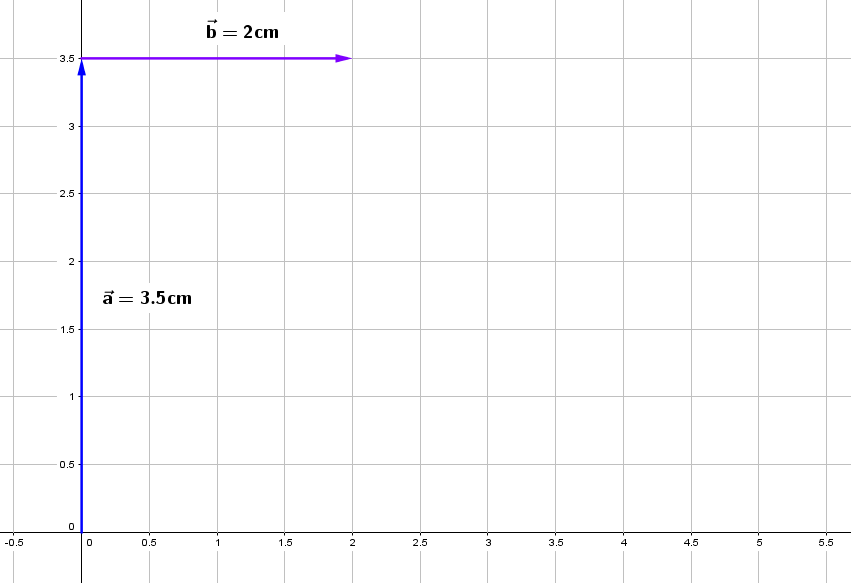
3.Se traza el vector $\overrightarrow{c}$ a partir de la punta de la flecha del vector $\overrightarrow{b}$. Recuerda que el sureste es 45º al sur del este.

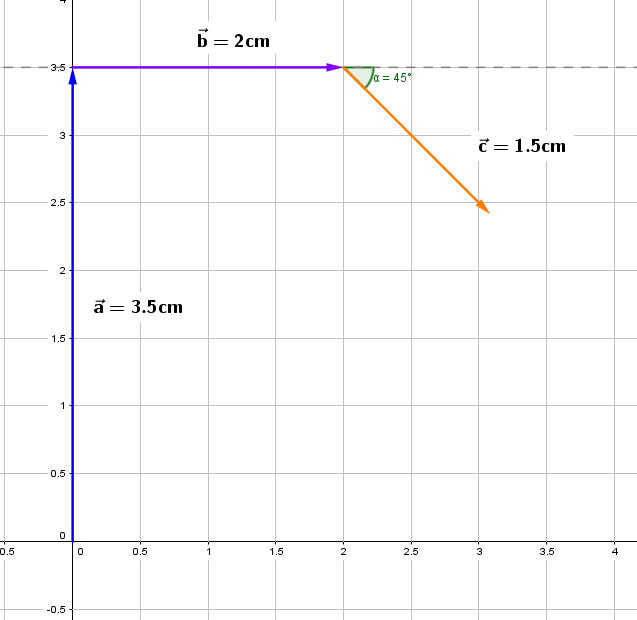
4.Se traza el vector $\overrightarrow{d}$ a partir de la punta de la flecha del vector $\overrightarrow{c}$.

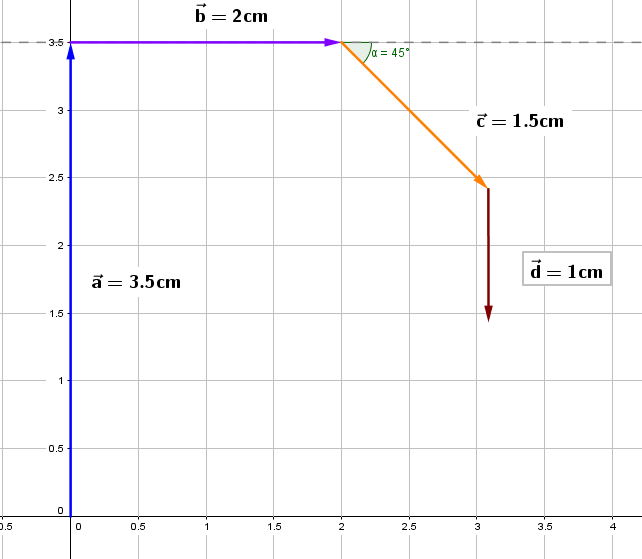
5.Se traza el vector resultante R a partir de la punta de la flecha del vector $\overrightarrow{d}$ al origen.

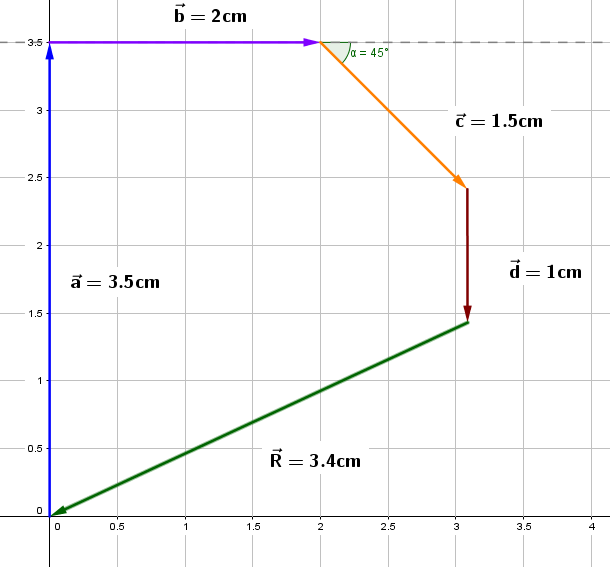
6.El vector resultante, que es el desplazamiento total, es de 340 m=3.4 cm

La distancia que recorre esta persona al caminar es de: d = 350 m+200 m+150 m+100 m = 900 m Distancia total recorrida = 900 m

También puedes verlo en este link: Ejemplo

Version Antigua