Potencia, trabajo y energía
Trabajo
Se realiza un trabajo siempre que una fuerza produzca un movimiento
Cuanto mayor sea la fuerza aplicada y mayor la distancia recorrida, mayor será el trabajo efectuado
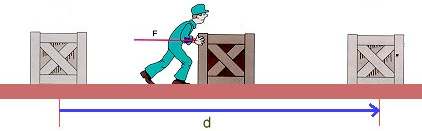
Donde: $$T = trabajo$$ $$F = magnitud\ de\ fuerza$$ $$d = magnitud\ del\ desplazamiento$$
Solo cuando la fuerza y el desplazamiento tienen la misma dirección y sentido
Joules (J)
Un Joule es el trabajo que debe realizarse para mover un cuerpo a lo largo de un metro aplicando una fuerza de un Newton
$$ Joule = \left( \text{Newton} \right)\left( \text{metro} \right)$$ $$1\ ft-lb = 1.36\ J$$
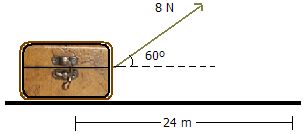
En este caso el trabajo dependerá del ángulo de la fuerza aplicada y de la dirección y sentido del desplazamiento
$$T = Fd\cos\theta$$
No se hace trabajo sobre el cuerpo si esta no se mueve (d=0)
El trabajo es cero, si la fuerza y el desplazamiento forman un ángulo de 90°
Ejemplo: Un hombre levanta a su compañera que tiene un peso de 52 kg hacia arriba en línea recta una distancia de 0.5 m, ¿Cuál es trabajo que realiza?
Si actúan sobre cuerpo varias fuerzas, se calcula el trabajo individual y luego se suman todos
Ejemplo: Se empuja un escritorio a una distancia de 2.5m a lo largo de una superficie horizontal por medio de una fuerza de 600N. La fuerza de fricción dinámica que aparece entre la mesa y la superficie es de 100N
Potencia
La rapidez con la que se realiza un trabajo $$P = \frac{T}{t}$$
La unidad de potencia en el SI es el Joule por segundo (J/s) llamada watt (W)
La potencia es de 1 W cuando se realiza un trabajo de 1 joule en 1 segundo $$1\ cv = 735\ W$$ $$1\ hp = 746\ W$$
Para fuerzas constantes, se puede expresar en función de la velocidad media
$$P = \frac{T}{t} = \frac{\text{Fd}}{t} = F\frac{d}{t}$$ $$P = Fv$$
Ejemplo: Una fuerza de 500N mantiene a un automóvil moviéndose a una velocidad media de 90 km/h en la misma dirección y sentido de la fuerza aplicada. ¿Cuál es la potencia del automóvil?
Energía
Capacidad de un cuerpo para llevar a cabo un trabajo, medida en Joules
Energía potencial
La energía potencial, es la que posee (almacena) un cuerpo debido a su posición o condición
Tiene el potencial para hacer un trabajo en un futuro
Puede deberse a su elevación, a su compresión o distensión, o a la posición de sus moléculas


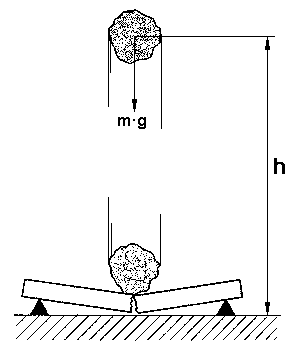
Si es debido a la elevación, se llamara energía potencial gravitacional
Mide el trabajo que se tuvo que realizar contra la gravedad para elevar un cuerpo

Definida matemáticamente por: $$E_{p} = mgh$$
Ejemplo: Una bolsa de 1 kg de arroz se encuentra en una alacena a 1.6 m del suelo. La superficie de una mesa está a 1.1 m sobre el suelo. ¿Cuál es la energía potencial gravitacional de la bolsa con respecto al suelo y con respecto a la mesa?
Energía Cinética
Es la que posee un cuerpo debido a su movimiento $$E_{c} = \frac{1}{2}mv^{2}$$
La energía cinética será 4 veces mayor a medida que aumente la velocidad

La energía cinética será mayor a medida que aumente la masa

1 joule corresponde a la energía de un cuerpo de 1 kg que se mueve a una rapidez de 1 m/s
Ejemplo: ¿Cuál es la energía cinética de un automóvil de 1400 kg que se mueve a una rapidez de 50 m/s (180 km/h)?
Energía Mecánica
La suma de la energía cinética y la energía potencial gravitacional $$E_{m} = E_{c} + E_{p}$$ $$E_{m} = \frac{1}{2}mv^{2} + mgh$$
Ejemplo: Calcula la energía mecánica de un pájaro de 350 g que viaja a 40 m/s y a una altura de 40m del piso