¿Sabías que puedes navegar las publicaciones deslizando a la izquierda y la derecha?

Movimiento Curvilíneo

03 Apr 2020 . category: 2doPeriodoFísica .
#rapidez #velocidad #curva #parábola #constante #posición #circunferencia #aceleración

Presentación electronica

Tiro horizontal

Un proyectil se desplaza horizontalmente a una rapidez constante al ir cayendo verticalmente con una aceleración g.

Justificaremos este comportamiento con un hecho experimental que, cuando son despreciables los efectos de fricción (rozamiento), un proyectil presenta dos movimientos perpendiculares al mismo tiempo: se mueve verticalmente con una aceleración descendente g y horizontalmente con una velocidad horizontal constante.

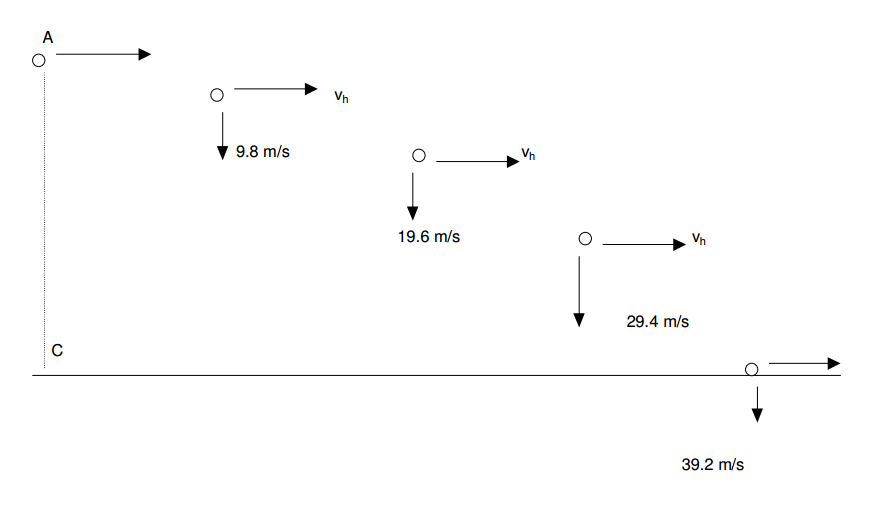
Se proyecta horizontalmente una pelota de béisbol en A con una velocidad de vh. Si la fricción del aire es despreciable, la pelota conserva la misma velocidad horizontal mientras no golpee algún objeto.

Al mismo tiempo, su velocidad vertical descendente aumenta 9.8 m/s cada segundo al producirse la caída libre.

El tiro horizontal se puede considerar como la composición de un movimiento horizontal rectilíneo uniforme y la caída libre.

El tiro horizontal es una combinación del movimiento rectilíneo uniforme y la caída libre pues la velocidad en “x” permanece constante, mientras que la velocidad en “y” comienza en cero y aumenta conforme el tiempo.

Las fórmulas a utilizar son las siguientes:

Para el movimiento horizontal “x”

$v_{x} = \frac{x}{t}$

En donde:

$x = \ alcance \ horizontal \ en \ m$

Para el movimiento vertical “y”

$v_{\text{fy}} = gt$ $y = \frac{1}{2}gt^{2}$ $v_{\text{fy}}^{2} = 2gy$

En donde:

$y = \ es \ la \ altura \ en \ metros$

Ejemplo:

Una pelota rueda sobre una mesa horizontal a 1.5 m de altura del suelo, cayendo por el borde de la misma. Si choca con el suelo a una distancia de 1.8m medidos horizontalmente desde el borde de la mesa, ¿con qué velocidad salió de la mesa?

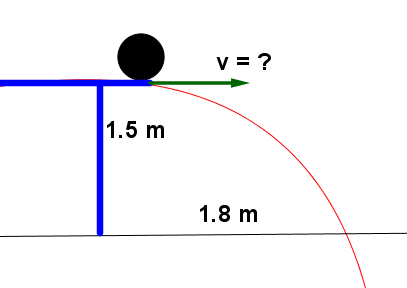
Solución:

Como se trata de un tiro horizontal, hemos de analizar por separado el movimiento horizontal “x” y el movimiento vertical “y”:

Horizontal: es un MRU y sólo contamos con la ecuación:

$v_{x} = \frac{x}{t}$

En donde podemos observar que nos falta el tiempo, por lo que quedará pendiente el cálculo de la velocidad.

Vertical: se trata de caída libre y con la altura de 1.5 m podemos calcular la velocidad final en “y” utilizando la ecuación:

$v_{\text{fy}}^{2} = 2gy$

Despejando

$v_{\text{fy}} = \sqrt{2gy}$ $v_{\text{fy}} = \sqrt{2\left( 9.8\ m/s^{2\ } \right)\left( 1.5m \right)} = 5.422\ m/s$

Con esta velocidad calculamos el tiempo que tarda la pelota en caer al suelo despejándolo de la ecuación:

$v_{\text{fy}} = gt$ $t = \frac{v_{\text{fy}}}{g}$ $t = \frac{5.422\ m/s}{9.8\ m/s^{2}} = 0.533s$

Calculamos la velocidad en “x”

$v_{x} = \frac{x}{t} = \frac{1.8\ m}{0.533\ s} = 3.377\ m/s$

Movimiento parabólico

El tiro parabólico completo se puede analizar como la composición de un movimiento horizontal rectilíneo uniforme y un tiro vertical hacia arriba, que no es más que un movimiento rectilíneo uniformemente acelerado hacia abajo.

En el tiro parabólico, un proyectil es lanzado con cierto ángulo de elevación y sometido únicamente a la fuerza constante de su peso, describe una trayectoria parabólica.

La velocidad del proyectil tiene en todo momento una componente horizontal y otra vertical. Si no se tiene en cuenta la fricción con el aire, la componente horizontal es constante en todo momento hasta que el proyectil alcanza el suelo.

Por lo contrario a causa de la fuerza de gravedad, el peso, el cambio de la componente vertical es continuo.

La suma de las componentes horizontal y vertical de la velocidad es un vector tangente en cualquier punto de la trayectoria del proyectil.

El tiro parabólico es un caso particular de un M.U.A. en dos dimensiones, la gravedad solo actúa en su movimiento a lo largo del eje Y, y el eje X no tiene aceleración alguna.

Por lo tanto, el movimiento de proyectiles es una combinación de dos movimientos, el movimiento a lo largo del eje X, es un M.R.U. y el movimiento a lo largo del eje Y es un M.U.A. cuya aceleración es –g.

Las expresiones que nos permiten conocer la ley de velocidades, ley de posiciones, altura máxima, alcance horizontal y componentes de la velocidad.

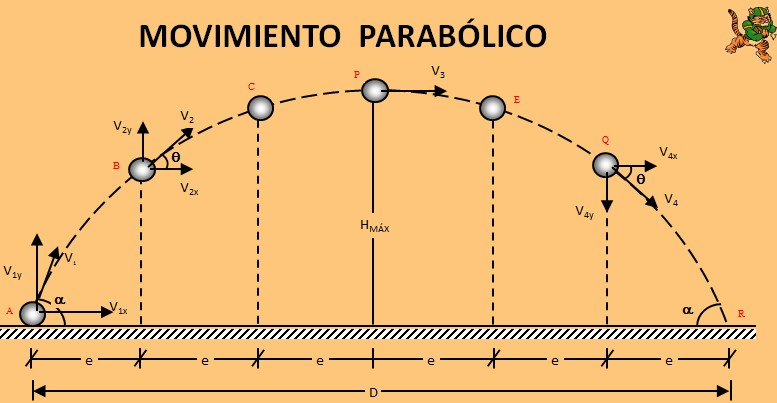
Dirección en el eje x

$x = v_{0x}t$ $v_{x} = v_{0x}$

Dirección en el eje y

$v_{y} = v_{0y} - gt$ $v_{y}^{2} = v_{0y}^{2} - 2gy$ $y = v_{0y}t - \frac{gt^{2}}{2}$

Ley de Velocidades:

$v = \left( v_{0}\cos\theta \right)i + \left( v_{0}\sin{\theta - gt} \right)j$

Ley de Posiciones:

$d = \left( v_{0}\cos\theta t \right)i + \left( v_{0}\sin\theta t - \frac{1}{2}gt^{2} \right)j$

Altura Máxima

$y_{\max} = \frac{v_{0y}^{2}}{2g} = \frac{\left( v_{0}\sin\theta \right)^{2}}{2g}$

Alcance horizontal

$x_{\max} = \frac{2v_{0x}v_{0y}}{g} = \frac{v_{0}^{2}\sin{2\theta}}{g}$

Componentes de la velocidad

$v_{0x} = v_{0}\cos\theta$ $v_{0y} = v_{0}\sin\theta$

Tiempo de subida

$t_{s} = \frac{v_{0y}}{g}$

Tiempo de vuelo

$T = t_{v} = 2t_{s}$

Ejemplo:

Un beisbolista golpea la pelota con una velocidad de 120 km/h, formando un ángulo de 60º con la horizontal. Determinar la altura máxima y la distancia horizontal alcanzada por la pelota.

Solución:

Datos

$v_{i} = 120\frac{\text{km}}{h} = 33.33\frac{m}{s}$ $g = 9.81\frac{m}{s^{2}}$ $\theta = 60^{\circ}$

Para la altura

$y_{\max} = \frac{v_{0y}^{2}}{2g} = \frac{\left( v_{0}\sin\theta \right)^{2}}{2g}$ $y_{\max} = \frac{\left\lbrack \left( 33.33\frac{m}{s} \right)\sin{60} \right\rbrack^{2}}{2\left( 9.81\frac{m}{s^{2}} \right)}$ $y_{\max} = \frac{833.16\frac{m^{2}}{s^{2}}}{19.62\frac{m}{s^{2}}}$ $y_{\max} = 42.46\ m$

Para el desplazamiento horizontal

$x_{\max} = \frac{v_{0}^{2}\sin{2\theta}}{g}$ $x_{\max} = \frac{\left( 33.33\frac{m}{s} \right)^{2}\ \sin{120}}{9.81\frac{m}{s^{2}}} = 98.06\ m$

Movimiento circular uniforme (MCU)

En este movimiento un cuerpo describe un movimiento circular cuando gira alrededor de un punto fijo central llamado eje de rotación. En el movimiento circular el origen del sistema de referencia se encuentra en el centro de la trayectoria circular. Ejemplos de este movimiento son las llantas de un automóvil, las hélices de los helicópteros, discos compactos y juegos mecánicos.

Este movimiento estudia los conceptos como velocidad angular, periodo y frecuencia.

Velocidad angular: La magnitud de la velocidad angular representa el cociente entre el valor del desplazamiento angular y el tiempo que tarda en efectuarlo:

$\omega = \frac{\theta}{t}$ $\omega = \frac{v}{r}$ $\omega = 2\pi f$

Donde:

$\omega = valor \ de \ la \ velocidad \ angular \ en \frac{\text{rad}}{s}$ $\theta = desplazamiento \ angular \ en \ rad$ $t = tiempo \ en \ el \ que \ se \ efectúa \ el \ desplazamiento \ en \ seg$ $v = velocidad \ lineal \ en \frac{m}{s}$ $r = radio \ de \ giro \ en \ m$ $f = frecuencia$

Período: Es el tiempo que tarda un cuerpo en dar una vuelta completa o en completar un ciclo.

$T = \frac{2\pi r}{v}$ $T = \frac{1}{f}$ $T = \frac{1}{n}$

Donde

$T = periodo \ dado \ en \ seg$ $n = numero \ de \ vueltas$

Frecuencia: Es el número de vueltas en la unidad de tiempo, es decir, es el inverso del periodo.

Ejemplo:

Un satélite artificial gira alrededor de la tierra en una órbita de 850 km, efectúa una vuelta completa en 103 minutos. ¿Cuál será la frecuencia y velocidad lineal? Calcular:

a) La frecuencia.

b) La velocidad angular.

Solución:

Datos

$r_{\text{tierra}} = 6370\ km$ $altura = 850\ km$ $r = 7220\ km$ $g = 9.81\frac{m}{s^{2}}$ $t = 103\min{= 6180\ s}$

Para la frecuencia, consideramos el periodo

$T = 6180s$ $f = \frac{1}{T} = \frac{1}{6180s} = 0.000616\ Hz$

Para la velocidad angular

$\omega = 2\pi f$ $\omega = 2\left( 3.1415926536\ rad \right)\left( 0.000161\frac{\text{ciclos}}{s} \right) = 0.00101\frac{\text{rad}}{s}$

Movimiento Circular Uniformemente acelerado

El movimiento circular uniformemente acelerado (MCUA) es un movimiento circular cuya aceleración angular α es constante.

Aceleración angular (α): es el cambio de velocidad angular en unidad de tiempo.

$\propto = \frac{\omega}{t} = \frac{\omega_{f} - \omega_{0}}{t}$

Nótese la similitud con las fórmulas del movimiento rectilíneo uniformemente acelerado (MRUA).

Las ecuaciones para el movimiento angular uniformemente acelerado son análogas a las del movimiento rectilíneo uniformemente acelerado, por lo que se tiene:

$\omega_{f} = \omega_{0} + at$ $\theta = \omega_{0}t + \frac{1}{2}at^{2}$ $\omega_{f}^{2} = \omega_{0}^{2} + 2a\theta$ $\omega_{m} = \frac{\omega_{f} + \omega_{i}}{2}$

Otro concepto importante es la aceleración lineal o tangencial, llamada así por ser tangente al movimiento. Produce variaciones en la velocidad lineal. Por ejemplo, si las ruedas de un auto irán con una aceleración angular α, entonces el auto adquirirá una aceleración tangencial o lineal perpendicular al movimiento de las ruedas que hará que el auto en su totalidad se mueva.

La relación entre la aceleración tangencial y la angular está dada por la siguiente ecuación:

$a_{T} = ra$

Donde

$a_{T} = aceleración \ tangencial \ en \frac{m}{s}$ $a = aceleración \ angular \ en \frac{\text{rad}}{s}$

Ejemplo:

Una rueda aumenta su velocidad angular de 30 rad/s a 80 rad/s en 5 s ¿Cuál es la aceleración angular?

Solución:

$\omega_{0} = 30\frac{\text{rad}}{s}$ $\omega_{f} = 80\frac{\text{rad}}{s}$ $t = 5s$

Formula

$a = \frac{\omega_{f} - \omega_{i}}{t}$ $a = \frac{80\frac{\text{rad}}{s} - 30\frac{\text{rad}}{s}}{5s}$ $a = 10\frac{\text{rad}}{s^{2}}$

Una esmeriladora que gira inicialmente con una velocidad angular de 8 rad/s recibe una aceleración constante de 2 $rad/s^2$ .

a) ¿Cuál será su desplazamiento angular en 8 s?

b) ¿Cuál es su velocidad angular final de ese tiempo?

c) ¿Cuál será su aceleración tangencial, si la rueda tiene un radio de 0.1m?

Version Antigua

Docente de Física 1 y TICs, Ing. en Computación egresado de la UNAM

Movimiento Curvilíneo

03 Apr 2020 . category: 2doPeriodoFísica . #rapidez #velocidad #curva #parábola #constante #posición #circunferencia #aceleración

Presentación electronica

Tiro horizontal

Movimiento parabólico

Movimiento circular uniforme (MCU)

Movimiento Circular Uniformemente acelerado

03 Apr 2020 . category: 2doPeriodoFísica .
#rapidez #velocidad #curva #parábola #constante #posición #circunferencia #aceleración